题目内容
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.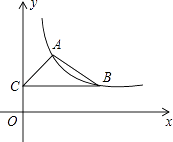
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.
【答案】
(1)解:∵反比例函数y= ![]() 的图象经过点A(1,2),
的图象经过点A(1,2),
∴k=1×2=2,
∴反比例函数解析式为y= ![]()
(2)解:∵点B(m,n)在反比例函数y= ![]() 的图象上,
的图象上,
∴mn=2.
又∵S△ABC= ![]() BC(yA﹣yB)=
BC(yA﹣yB)= ![]() m(2﹣n)=m﹣
m(2﹣n)=m﹣ ![]() mn=m﹣1=2,
mn=m﹣1=2,
∴m=3,n= ![]() ,
,
∴点B的坐标为(3, ![]() ).
).
(3)解:将A(1,2)代入y=ax﹣1中,
2=a﹣1,解得:a=3;
将B(3, ![]() )代入y=ax﹣1中,
)代入y=ax﹣1中,
![]() =3a﹣1,解得:a=
=3a﹣1,解得:a= ![]() .
.
∵直线y=ax﹣1与线段AB交于点P,P为线段AB上一动点(P不与A、B重合),
∴ ![]() <a<3.
<a<3.
【解析】(1)利用待定系数法把A坐标代入即可;(2)运用三角形面积公式,把高转化为(yA﹣yB);(3)a代表斜率,因此把两个端点代入解析式,得出斜率的两个极端的范围.

练习册系列答案
相关题目