题目内容
【题目】如图，在
中，
，
，AD是的角平分线，
，垂足为E．
求证：
；
已知
，求AC的长；
求证：
．
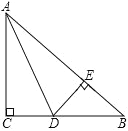
【答案】（1）证明见解析；（2）
；（3）证明见解析.
【解析】
（1）先根据题意判断出△ABC是等腰直角三角形，故
，再由
可知△BDE是等腰直角三角形，故DE
，再根据角平分线的性质即可得出结论；
（2）由（1）知，△BDE是等腰直角三角形，DE=BE=CD，再根据勾股定理求出BD的长，进而可得出结论；
（3）先根据HL定理得出Rt△ACD≌Rt△AED，故AE
，再由CD=BE可得出结论．
证明：
在
中，
，
，
是等腰直角三角形，
，
，
是等腰直角三角形，
．
是的角平分线，
，
；
解：由知，
是等腰直角三角形，
，
，
，
；
证明：是的角平分线，，
．
在
与
中，
，
≌，
．
由知
，
．
故答案为：（1）证明见解析；（2）；（3）证明见解析.
练习册系列答案
相关题目
【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟） | 里程数（公里） | 车费（元） | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？
