题目内容
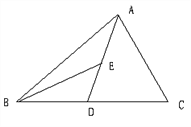
【题目】看图填空,并在括号内说明理由: 如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
证明:∵∠BAP与∠APD互补(_________), ∴AB∥CD(____________),
∴∠BAP=∠APC(__________).
又∵∠1=∠2(__________),
∴∠BAP﹣∠1=∠APC﹣∠2(_________),即∠3=∠4,
∴AE∥PF,(___________),
∴∠E=∠F(__________).

【答案】 已知; 同旁内角互补,两直线平行; 两直线平行,内错角相等; 已知; 等量代换; 内错角相等,两直线平行; 两直线平行,内错角相等.
【解析】证明:∵∠BAP与∠APD互补(已知), ∴AB∥CD(同旁内角互补,两直线平行),
∴∠BAP=∠APC( 两直线平行,内错角相等).
又∵∠1=∠2(已知),
∴∠BAP﹣∠1=∠APC﹣∠2(等量代换),即∠3=∠4,
∴AE∥PF,(内错角相等,两直线平行),
∴∠E=∠F( 两直线平行,内错角相等).

练习册系列答案
相关题目