题目内容
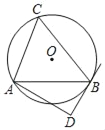
【题目】如图,直线![]() 相交于
相交于![]() ,在直线
,在直线![]() 上分别取点
上分别取点![]() ,使
,使![]() ,分别过点A,B作直线
,分别过点A,B作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,设
,设![]() .
.
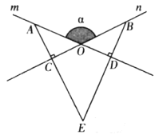
(1)求证:![]() ;
;
(2)小明说,不论![]() 是锐角还是钝角,点
是锐角还是钝角,点![]() 都在
都在![]() 的平分线上,你认为他说的有道理吗?并说明理由.
的平分线上,你认为他说的有道理吗?并说明理由.
(3)连接![]() ,当
,当![]() 与三角板的形状相同时,直接写出
与三角板的形状相同时,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)小明的说法正确.见解析;(3)60°,120°,90°.
【解析】
(1)通过证明![]() 即可得证;
即可得证;
(2)由(1)得OC=OD,再利用角平分线的判定即可得证;
(3)连接![]() ,当
,当![]() 与三角板的形状相同时,
与三角板的形状相同时,![]() 的锐角可能为30°,60°,45°,再证∠COE=∠DOE,最后利用对顶角相等即可求得答案.
的锐角可能为30°,60°,45°,再证∠COE=∠DOE,最后利用对顶角相等即可求得答案.
(1)证明:∵AC⊥BC,AD⊥BD,
∴∠ACO=∠BDO=90°
在![]() 与
与![]() 中,
中,
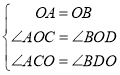
![]() (AAS),
(AAS),
![]()
(2)由(1)可知![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() 点
点![]() 在
在![]() 的平分线上,
的平分线上,
![]() 与
与![]() 是锐角还是钝角没有关系,
是锐角还是钝角没有关系,
∴不论![]() 是锐角还是钝角,点
是锐角还是钝角,点![]() 都在
都在![]() 的平分线上.
的平分线上.
∴小明的说法正确.
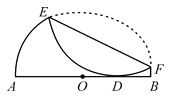
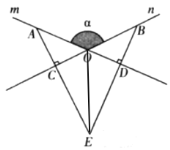
(3)如图,由(2)得OE平分∠CED,
∴∠CEO=∠OED,
又∵∠ECO=∠ODE=90°,
∴∠COE=∠DOE,
∴![]() =∠COD=2∠COE,
=∠COD=2∠COE,
当∠COE=30°时,![]() =60°,
=60°,
当∠COE=60°时,![]() =120°,
=120°,
当∠COE=45°时,![]() =90°,
=90°,
综上所述,![]() 的值为:60°,120°,90°.
的值为:60°,120°,90°.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目