��Ŀ����
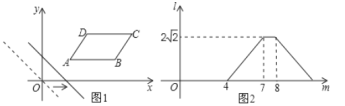
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A�������ǣ�4��0��������OA��OC��4OB������P�ڹ�A��B��C������������ϣ�
��1���������ߵĽ���ʽ��
��2���Ƿ���ڵ�P��ʹ�á�ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱ��y���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF���е�GΪԲ�ģ���EFΪֱ������G������G��Сʱ�������P�����꣮

���𰸡���1��y����x2+3x+4����2�����ڣ�P�������ǣ�2��6����2����6������3�� ��
��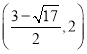
��������
��1�����ȸ�������ó�C��B�����꣬�����ô���ϵ����������κ�������ʽ���ɣ�
��2���ֱ����õ�һ�����������CΪֱ�Ƕ���ʱ���ڶ������������AΪֱ�Ƕ���ʱ���ó�P�����꼴�ɣ�
��3�����ݴ��߶���̣��ɵõ�OD��ACʱ��OD��̣���EF��̣������ó�P�����꼴�ɣ�
�⣺��1����A��4��0������֪OA��4��
��OA��OC��4OB��
��OA��OC��4��OB��1��
��C��0��4����B����1��0����
�������ߵĽ���ʽ��y��ax2+bx+c��
�� ��
��
��ã�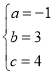 ��
��
�������ߵĽ���ʽ�ǣ�y����x2+3x+4��
��2�����ڣ�
��һ���������ͼ1������CΪֱ�Ƕ���ʱ������C��CP1��AC�����������ڵ�P1��
����P1��y��Ĵ��ߣ�������M��
�ߡ�ACP1��90����
���MCP1+��ACO��90����
�ߡ�ACO+��OAC��90����
���MCP1����OAC��
��OA��OC��
���MCP1����OAC��45����
���MCP1����MP1C��
��MC��MP1��
��P��m����m2+3m+4������m����m2+3m+4��4��
��ã�m1��0����ȥ����m2��2��
����m2+3m+4��6��
��P��2��6����
�ڶ����������ͼ1������AΪֱ�Ƕ���ʱ����A��AP2��AC���������ڵ�P2��
����P2��y��Ĵ��ߣ�������N��AP��y���ڵ�F��
��P2N��x�ᣬ
����CAO��45����
���OAP��45����
���FP2N��45����AO��OF��
��P2N��NF��
��P2��n����n2+3n+4������n������n2+3n+4��+4��
��ã�n1����2��n2��4����ȥ����
����n2+3n+4����6��
��P2�������ǣ���2����6����
����������P�������ǣ�2��6����2����6����
��3����ͼ2������OD���������֪���ı���OFDE�Ǿ��Σ���OD��EF��
���ݴ��߶���̣��ɵõ�OD��ACʱ��OD��̣���EF��̣�
�ɣ�1����֪����ֱ����AOC�У�OC��OA��4��
��AC��![]() ��4
��4![]() ��
��
���ݵ��������ε����ʣ�D��AC���е㣮
����DF��OC��
��DF��![]() OC��2��
OC��2��
����P����������2��
��x2+3x+4��2��
��ã�x��![]() ��
��
����EF���ʱ��Բ��С����P�������ǣ� ��
��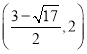 ��
��



 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�