题目内容
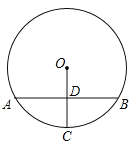
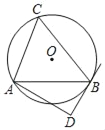
【题目】如图，⊙O的半径为5，△ABC是⊙O的内接三角形，AB＝8．AD和过点B的切线互相垂直，垂足为D．
（1）求证：∠BAD+∠C＝90°；
（2）求线段AD的长．
【答案】（1）证明见解析；（2）6.4
【解析】
（1）连接BO延长交⊙O于E，连接AE，根据切线的性质、结合题意得到AD∥BE，根据平行线的性质、圆周角定理证明；
（2）证明△ABE∽△DAB，根据相似三角形的性质得到比例式，计算即可．
（1）连接BO延长交⊙O于E，连接AE，
∵DB为⊙O的切线，
∴EB⊥BD，
∵AD⊥BD，
∴AD∥BE，
∴∠BAD＝∠EBA，
∵BE为直径，
∴∠EBA+∠E＝90°，
由圆周角定理得，∠E＝∠C，
∴∠BAD+∠C＝90°；
（2）∵⊙O的半径为5，
∴BE＝10．
∵∠BAD＝∠EBA，∠D＝∠BAE，
∴△ABE∽△DAB，
∴
，
∵AB＝8，BE＝10，
∴AD＝6.4，
∴线段AD的长度为6.4．
练习册系列答案
相关题目
【题目】焦作市教育局为调查全市教师的运动情况，结合现今流行的“微信运动”，随机调查了本市
名老师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表：
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
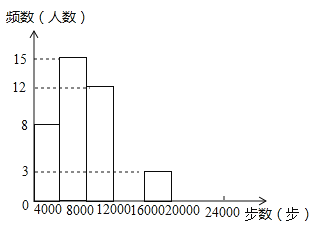
请根据以上信息，解答下列问题：
（1）写出
的值，并补全频数分布直方图；
（2）本市约有
名教师，结合调查的数据估计日行走步数超过
步（包含步）的教师有多少名？
（3）若在被调查的教师中，选取日行走步数超过
步（包含步）的两名教师与大家分享心得，求被选取的两名教师恰好都在
步（包含步）以上的概率．
