题目内容
【题目】如图,□OABC的三个顶点分别为O(0,0),C(4,0),B(3,3),∠AOC的平分线OP交AB于点P,则点P的坐标为______________.

【答案】(![]() ,3).
,3).
【解析】
过点P作PE⊥x轴,PF⊥AO,垂足分别为点E、F,根据角平分线的性质得PE=PF,设OE=x,则OF=x,用含有x的代数式分别表示AF、PF和AP,然后利用勾股定理求解即可.
过点P作PE⊥x轴,PF⊥AO,垂足分别为点E、F,如图所示,
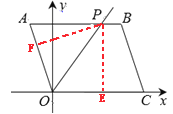
∵四边形ABCD是平行四边形,且B(3,3),C(4,0)
∴AB=OC=4,AO=BC=![]() ,
,
∴A(-1,0),
∴PE=3,
∵OP是∠AOC的平分线,
∴PE=PF=3,OE=OF,
设OE=x,则OF=x,AF=![]() -x,AP=x+1,
-x,AP=x+1,
在Rt△APF中,![]() ,
,
∴![]() ,解得x=
,解得x=![]() .
.
∴点P 的坐标为(![]() ,3).
,3).
故答案为:(![]() ,3).
,3).

练习册系列答案
相关题目