题目内容
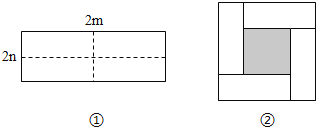
【题目】如图①所示是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法表示图②中阴影部分的面积.
方法① ;方法② .
(3)观察图②,请写出(m+n)2、(m﹣n)2、mn这三个代数式之间的等量关系: .
(4)若a+b=6,ab=5,则求a﹣b的值.
【答案】(1)m﹣n (2)(m+n)2﹣4mn;(m﹣n)2 (3)(m﹣n)2=(m+n)2﹣4mn (4)±4
【解析】
平均分成后,每个小长方形的长为m,宽为n.
(1)正方形的边长=小长方形的长﹣宽;
(2)第一种方法为:大正方形面积﹣4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(3)利用(2)中两种不同的方法表示的是同一个图形的面积解答即可;
(4)利用(a﹣b)2=(a+b)2﹣4ab可求解.
解:(1)图②中的阴影部分的小正方形的边长=m﹣n;
(2)方法①(m+n)2﹣4mn;方法②(m﹣n)2;
(3)这三个代数式之间的等量关系是:(m﹣n)2=(m+n)2﹣4mn;
(4)∵(a﹣b)2=(a+b)2﹣4ab,a+b=6,ab=5,
∴(a﹣b)2=36﹣20=16,
∴a﹣b=±4.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】下表是小明记录的今年雨季一周河水的水位变化情况(上周末的水位达到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | +0.20 | +0.81 | ﹣0.35 | +0.03 | +0.28 | ﹣0.36 | ﹣0.01 |
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
(2)与上周相比,本周末河流水位是上升了还是下降了?