题目内容
【题目】已知,![]() 与
与![]() 两角的角平分线交于点
两角的角平分线交于点![]() ,
,![]() 是射线
是射线![]() 上一个动点,过点
上一个动点,过点![]() 的直线分别交射线
的直线分别交射线![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
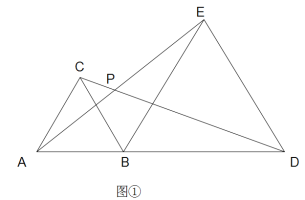
(1)如图1,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
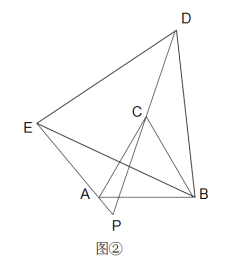
(2)如图2,若![]() ,请探索
,请探索![]() 与
与![]() 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;
(3)在点![]() 运动的过程中,请直接写出
运动的过程中,请直接写出![]() ,
,![]() 与
与![]() 这三个角之间满足的数量关系:_________________________________.
这三个角之间满足的数量关系:_________________________________.


【答案】(1)![]() ;(2)
;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]() 或
或![]()
【解析】
(1)根据角平分线的性质结合三角形外角的性质即可求解;
(2)设![]() ,
,![]() ,根据角平分线的性质结合四边形内角和定理即可求解;
,根据角平分线的性质结合四边形内角和定理即可求解;
(3)分点P在线段BD上和点P在线段BD的延长线上两种情况讨论即可求解.
(1)∵PA、PB是∠BAM、∠ABN的角平分线,
∴∠BAP=∠PAE=![]() ∠BAM=
∠BAM=![]() ,
,
∠ABP=∠PBE=![]() ∠ABN=
∠ABN=![]() ,
,
∴∠BPC=∠BAP+∠ABP=![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵PA、PB是∠BAM、∠ABN的角平分线,
∴设![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)∵PA、PB是∠BAM、∠ABN的角平分线,
∴设![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
如图,当点P在线段BD上时,

![]() ,
,
∴![]() ;
;
如图,当点P在线段BD的延长线上时,
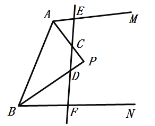
![]() ,即
,即![]() ,
,
∴![]() ,
,
即![]() ;
;

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
【题目】“品中华诗词,寻文化自信”.某校组织全校1000名学生举办了第二届“中华诗词大赛”的初赛,从中抽取部分学生的成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩 | 人数 | 百分比 |
|
| 8 | 20% |
|
| 16 |
|
|
|
| 30% |
|
| 4 | 10% |
频数分布直方图

请观察图表,解答下列问题:
(1)表中![]() __________,
__________,![]() __________;
__________;
(2)补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,那么请你估计该校进入决赛的学生大约有多少人?