题目内容
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=a.
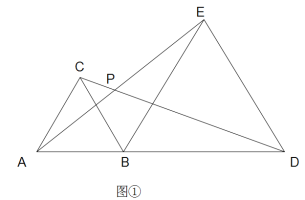
(1)当a=60°, 如图①则,∠DPE的度数______________
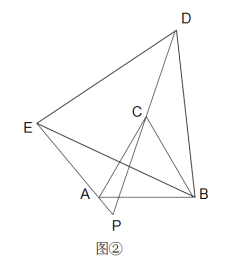
(2)若△BDE绕点B旋转一定角度,如图②所示,求∠DPE(用a表示)
【答案】(1)60°;(2)∠DPE=a
【解析】
(1)利用SAAS证得△ABE≌△CBD,利用全等三角形的性质得到∠AEB=∠CDB,再利用三角形内角和定义以及等边三角形的性质即可解答;
(2)利用SAAS证得△ABE≌△CBD,利用全等三角形的性质得到∠AEB=∠BDC,再利用三角形内角和定理即可完成.
(1)解:∵∠ABC=∠DBE
∴∠ABC+∠CBE=∠DBE+∠CBE
即∠ABE=∠CBD
在△ABE和△CBD中

∴△ABE≌△CBD(SAS)
∴∠AEB=∠CDB
∵∠ABC=∠DBE,AB=CB, BD=BE
∴△ABC和△EBD是等边三角形
∴∠BDE=∠EDB=60°
∵∠EDP+∠CDB=60°
∴∠EDP+∠AEB=60°
∵∠DPE+∠AEB+∠BED+∠EDP=180°
∴∠DPE=60°
故答案为:60°
(2)如图:
∵∠ABC=∠DBE=a
∴∠ABC﹣∠EBC=∠DBE﹣∠EBC
即∠ABE=∠CBD
在△ABE和△CBD中

∴△ABE≌△CBD(SAS)
∴∠AEB=∠BDC
∵∠DQB+∠DBE+∠BDC=180°
∠EQP+∠DPE+∠AEB=180°
又∵∠DQB=∠EQP
∴∠DBE=∠DPE
∴∠DPE=a


练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目