题目内容
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)a,b是有理数,则a-2,b+3都是有理数,根据如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0即可确定;
(2)首先把已知的式子化成mx+n=0,(其中a、b为有理数,x为无理数)的形式,根据m=0且n=0即可求解.
解:(1)![]() 整理得:
整理得:![]() ,
,
∵a、b为有理数,则a-2,b+3都是有理数,而![]() 为无理数,根据题意如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0,
为无理数,根据题意如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0,
对比形式可知m为![]() =0且n为
=0且n为![]() =0,则
=0,则![]() ,
,![]() ;
;
(2)整理,得:![]() ,
,
∵a、b为有理数,同(1)中理可得:![]() ,
,
解得: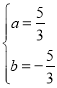 ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人.行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
5 | 2 | -4 | -3 | 10 |
(1)接送完第5批客人后,该驾驶员在公司 边(填南或北),距离公司 千米.
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油 升.
(3)若该出租车的计价标准为:行驶路程不超过3![]() 收费10元,超过3
收费10元,超过3![]() 的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?