题目内容
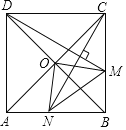
【题目】如图,在矩形纸片 ABCD 中,AD=5cm,AB=4cm,将矩形纸片 ABCD 沿直线l 折叠,使点 A 落在边 BC 上的 A'处,当直线 l 恰好过点 D 时,用直尺和圆规在图中作出直线 l,(保留作图 痕迹,不写作法),设点 A'与点 B 的距离为 x cm.并求出 x 的值.

【答案】作图见解析,2.
【解析】
以D为圆心、DA为半径画弧交BC于A′,连接AA′,分别以A,A′为圆心,大于![]() AA′为半径交于两点,连接两点即可,然后根据数据求出x即可.
AA′为半径交于两点,连接两点即可,然后根据数据求出x即可.
解:如图,以D为圆心、DA为半径画弧交BC于A′,连接AA′,分别以A,A′为圆心,大于![]() AA′为半径交于两点,连接两点,得到直线l,直线l即为所求,
AA′为半径交于两点,连接两点,得到直线l,直线l即为所求,
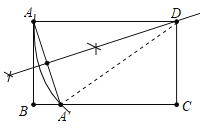
连接DA′,
∵四边形ABCD为矩形,
∴DC=AB=4cm,BC=AD=5cm,
∵折叠,
∴DA′=DA =5cm,
CA′=![]() ,
,
∴BA′=BC-CA′=5-3=2cm,
即x=2.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】将正偶数按下表排成5列:
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
第一行 | 2 | 4 | 6 | 8 | |
第二行 | 16 | 14 | 12 | 10 | |
第三行 | 18 | 20 | 22 | 24 | |
第四行 | 32 | 30 | 28 | 26 | |
…… |
根据上面规律,2020应在( )
A.125行,3列B.125行,2列C.253行,2列D.253行,3列