题目内容
【题目】如图，已知二次函数y= 
x2﹣4的图象与x轴交于A，B两点，与y轴交于点C，⊙C的半径为 
，P为⊙C上一动点．
（1）点B，C的坐标分别为B（），C（）；
（2）是否存在点P，使得△PBC为直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；
（3）连接PB，若E为PB的中点，连接OE，则OE的最大值= ．
【答案】
（1）3，0；0，﹣4
（2）
存在点P，使得△PBC为直角三角形，
①当PB与⊙相切时，△PBC为直角三角形，如图（2）a，
连接BC，
∵OB=3．OC=4，
∴BC=5，
∵CP2⊥BP2，CP2= 
，
∴BP2=2 ，
过P2作P2E⊥x轴于E，P2F⊥y轴于F，
则△CP2F∽△BP2E，四边形OCP2B是矩形，
∴ 
= 
=2，
设OC=P2E=2x，CP2=OE=x，
∴BE=3﹣x，CF=2x﹣4，
∴ 
= 
=2，
∴x= 
，2x= 
，
∴FP2= ，EP2= ，
∴P2（ ，﹣ ），
过P1作P1G⊥x轴于G，P1H⊥y轴于H，
同理求得P1（﹣1，﹣2），
②当BC⊥PC时，△PBC为直角三角形，
过P4作P4H⊥y轴于H，
则△BOC∽△CHP4，
∴ 
= 
= 
，
∴CH= 
，P4H= 
，
∴P4（ ，﹣ ﹣4）；
同理P3（﹣ ， ﹣4）；
综上所述：点P的坐标为：（﹣1，﹣2）或（ ，﹣ ）或（ ，﹣ ﹣4）或（﹣ ， ﹣4）；
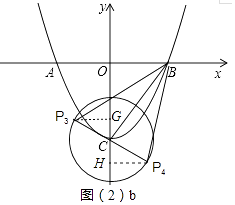
（3）
【解析】解：（1）在y= 
x2﹣4中，令y=0，则x=±3，令x=0，则y=﹣4，
∴B（3，0），C（0，﹣4）；
所以答案是：3，0；0，﹣4；
如图（3），当PB与⊙C相切时，PB与y 轴的距离最大，OE的值最大，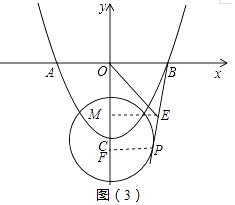
∵过E作EM⊥y轴于M，过P作PF⊥y轴于F，
∴OB∥EM∥PF，
∵E为PB的中点，
∴ME= 
（OB+PF）= 
，OM=MF= OF= ，
∴OE= 
= ．
所以答案是： ．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．
