题目内容
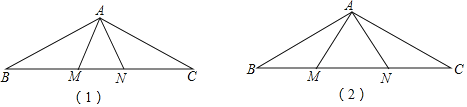
【题目】已知如图,M、N是△ABC的BC边上两点,且AB=AC,BM=CN
(1)如图1,证明:△ABN≌△ACM;
(2)如图2,当∠ANB=2∠B时,直接写出图中所有等腰三角形(△ABC除外)
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据SAS证明△ABN≌△ACM即可;
(2)利用全等三角形的性质,三角形的外角的性质可以证明△AMN,△ANC,△ABM是等腰三角形;
(1)证明:∵AC=AB,
∴∠B=∠C,
又∵BM=CN,
∴BM+MN=CN+MN
∴BN=CM
在△ABN和△ACM中,
 ,
,
∴△ABN≌△ACM(SAS).
(2)∵△ABN≌△ACM,
∴∠ANB=∠AMC,
∴AM=AN,
∴△AMN是等腰三角形,
∵∠ANB=2∠B=2∠C=∠C+∠CAN,
∴∠C=∠CAN,
∴△ANC是等腰三角形,同法可证△ABM是等腰三角形.

练习册系列答案
相关题目




