题目内容
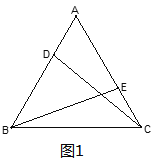
【题目】如图,在边长为8的等边三角形ABC中,点D沿射线AB方向由A向B运动,点F同时从C出发,以相同的速度每秒1个单位长度沿射线BC方向运动,过点D作DE⊥AC,连结DF交射线AC于点G.
(1)当DF⊥AB时,求AD的长;
(2)求证:EG=![]() AC.
AC.
(3)点D从A出发,经过几秒,CG=1.6?直接写出你的结论.

【答案】(1)![]() ;(2)详见解析;(3)t=4.8s或11.2s时,CG=1.6.
;(2)详见解析;(3)t=4.8s或11.2s时,CG=1.6.
【解析】
(1)设AD=x,根据直角三角形的性质列出方程,解方程即可;
(2)过点D作DH∥BC,交AC于点H,则∠HDG=∠F,先判定△ADH是等边三角形,再根据等量代换得到DH=FC,进而判定△DHG≌△FCG(AAS),得到HG=CG,再根据△ADH为等边三角形,DE⊥AH,得出AE=EH,最后得出AC=AH+CH=2EH+2HG=2EG;
(3)分两种情形解答即可;
解:(1)设AD=x,则CF=x,BD=8﹣x,BF=8+x,
∵DF⊥AB,∠B=60°,
∴BD=![]() BF,即8﹣x=
BF,即8﹣x=![]() (8+x),
(8+x),
解得,x=![]() ,即AD=
,即AD=![]() ;
;
(2)如图所示,过点D作DH∥BC,交AC于点H,则∠HDG=∠F,

∵△ABC是等边三角形,
∴∠ADH=∠AHD=∠A=60°,
∴△ADH是等边三角形,
∴AD=DH,
又∵点D与F的运动速度相同,
∴AD=CF,
∴DH=FC,
在△DHG和△FCG中,
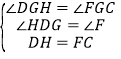 ,
,
∴△DHG≌△FCG(AAS),
∴HG=CG,
∵△ADH为等边三角形,DE⊥AH,
∴AE=EH,
∴AC=AH+CH=2EH+2HG=2EG,
∴EG=![]() AC.
AC.
(3)由(2)可知CG=GH=1.6,
∴AD=AH=8﹣3.2=4.8或AD=AH=8+3.2=11.2,
∴t=4.8s或11.2s时,CG=1.6.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目