题目内容
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
【答案】
(1)证明:连接OD,在△AOD中,OA=OD,
∴∠A=∠ODA,
又∵∠A+∠CDB=90°
∴∠ODA+∠CDB=90°,
∴∠BDO=180°-90°=90°,即OD⊥BD,
∴BD与⊙O相切.
(2)解:连接DE,∵AE是⊙O的直径,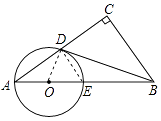
∴∠ADE=90°,
∴DE∥BC.
又∵D是AC的中点,
∴AE=BE.
∴△AED∽△ABC.
∴AC∶AB=AD∶AE.
∵AD:AE=4:5
∴AC∶AB=4∶5,
令AC=4x,AB=5x,则BC=3x.
∵BC=6,
∴AB=10,
∴AE=5,
∴⊙O的直径为5.
【解析】 (1)连接OD,根据同圆的半径相等得出OA=OD, 根据等边对等角得出∠A=∠ODA,根据等量代换及平角的定义得出∠BDO=90°,从而得出BD与⊙O相切;
(2)(1)连接DE,根据直径所对的圆周角是直角得出∠ADE=90°,根据同位角相等两直线平行得出DE∥BC.根据三角形中位线的判定知AE=BE,从而判断出△AED∽△ABC,根据相似三角形对应边成比例得出AC∶AB=AD∶AE,从而找到AC,AB的关系,从而得出该圆的直径。

【题目】某童装店有A、B两种型号的童装,其进价与售价如下表所示:
型号 | 进价(元) | 售价(元) |
A型 | 90 | 108 |
B型 | 100 | 130 |
根据市场需要,服装店决定:购进A种服装的数量要比购进B种服装的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总利润不少于699元.若假设购进B种服装x件,那么:
(1)请写出A、B两种服装全部销售完毕后的总利润y/元用含x/件的式子表示;
(2)请问该服装店有几种满足条件的进货方案?哪种方案获利最多?