��Ŀ����
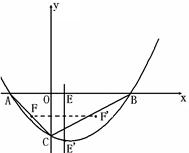
��֪��������y1=��2x2��2��ֱ��y2=2x+2�ཻ
��A�͵�B��
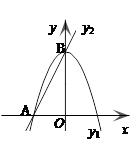
��1�������A�͵�B�����ꡣ
��2���۲�ͼ����ֱ��д��y1��y2���Ա���x��ȡֵ��Χ��
��3����x��ȡһֵʱ,x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2.��y1��y2��
ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M= y1=y2.�����磺��x=1ʱ��y1=0,y2=4,y1��y2����ʱM=0.�� ��ʹ��M=1��xֵ������
��A�͵�B��

��1�������A�͵�B�����ꡣ
��2���۲�ͼ����ֱ��д��y1��y2���Ա���x��ȡֵ��Χ��
��3����x��ȡһֵʱ,x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2.��y1��y2��
ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M= y1=y2.�����磺��x=1ʱ��y1=0,y2=4,y1��y2����ʱM=0.�� ��ʹ��M=1��xֵ������
��1��A��-1,0��B��0,2����2��-1<x<0��3��1
�����������1����������������ཻ�����У�
��2x2��2 =2x+2
����x=0��x=-1
��A��-1,0��B��0,2��
��2��ͨ��ͼ������ɵã���-1<x<0ʱ��������
��3���������֪����ȡֵ��Сʱ������������M=1ʱ��
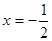 ����ʱͼ�εķ�����
����ʱͼ�εķ�������������ʽ���ʱx=0��x=-1
����������
�������ڽ���ʱҪ�������ö��κ�����ͼ�������������κ����Ľ���ʽ���������ν��˼������DZ���Ĺؼ���,

��ϰ��ϵ�д�
�����Ŀ
 ��x�ύA��B���㣨A����B����ࣩ��ֱ��
��x�ύA��B���㣨A����B����ࣩ��ֱ�� �������߽���A��C���㣬����C��ĺ�����Ϊ2��
�������߽���A��C���㣬����C��ĺ�����Ϊ2��
 ���ƽ���߽���������E�㣬���߶�PE���ȵ����ֵ��
���ƽ���߽���������E�㣬���߶�PE���ȵ����ֵ�� ����A��-1��0����B��4��0����P��5��3������������y�ύ�ڵ�C��
����A��-1��0����B��4��0����P��5��3������������y�ύ�ڵ�C��
 ��
�� ��Ϊ���㣬�ҹ�B��
��Ϊ���㣬�ҹ�B�� ��
�� ��
�� ��
�� ��
�� �������
�������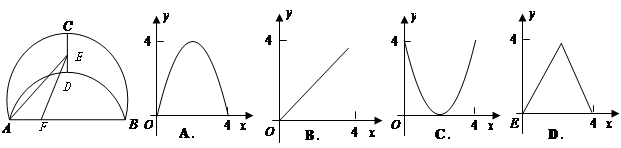
 ��ͼ��Ϊ�����ߣ���x����A��B���㣬��y����C�㣮����AC=
��ͼ��Ϊ�����ߣ���x����A��B���㣬��y����C�㣮����AC=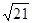 ��BC=
��BC=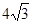 ��
��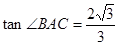 ��
��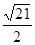 ����λ���ٶ�����AC���C�����˶�������ͬʱ������������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�������E��AB�Ĵ���
����λ���ٶ�����AC���C�����˶�������ͬʱ������������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�������E��AB�Ĵ���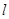 ���������ڵ�E�䣬����F����ֱ��
���������ڵ�E�䣬����F����ֱ��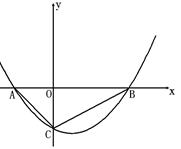
 ��Ԫ������������y������֮���ϵΪy=
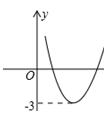
��Ԫ������������y������֮���ϵΪy=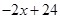 ��������������P��Ԫ���������۵���
��������������P��Ԫ���������۵���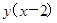 ���������۵���Ϊ����ʱ��ÿ�ջ������48Ԫ���ұ�֤��������������10����
���������۵���Ϊ����ʱ��ÿ�ջ������48Ԫ���ұ�֤��������������10����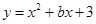 �ĶԳ���Ϊ
�ĶԳ���Ϊ ����
����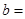 ��
��