题目内容
(本题满分12分,其中第(1)小题5分,第(2)小题4分,第(3)小题3分)
已知抛物线 过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.
过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.

(1)求二次函数的解析式;
(2)求tan∠APC的值;
(3)在抛物线上求一点Q,过Q点作x轴的垂线,垂足为H,使得∠BQH=∠APC.
已知抛物线
 过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.
过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.
(1)求二次函数的解析式;
(2)求tan∠APC的值;
(3)在抛物线上求一点Q,过Q点作x轴的垂线,垂足为H,使得∠BQH=∠APC.
(1)y=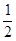 x2-
x2-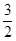 x-2 (2)tan∠APC=
x-2 (2)tan∠APC=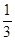 (3)Q(-7,33).
(3)Q(-7,33).
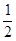 x2-
x2-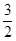 x-2 (2)tan∠APC=
x-2 (2)tan∠APC=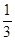 (3)Q(-7,33).
(3)Q(-7,33).试题分析:解:(1)∵抛物线y=ax2+bx+c经过点A(-1,0),B(4,0),P(5,3)
∴
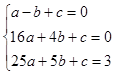 ,解得
,解得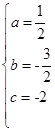 (4分)
(4分)∴抛物线的解析式
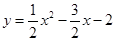 (1分)
(1分)(2)∵抛物线与y轴交于点C,∴C(0,-2) (1分)
∵A(-1,0),P(5,3),∴
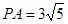 ,
,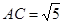 ,
,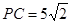 (1分)
(1分)∵
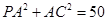 ,
,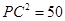 ,∴
,∴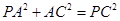 (1分)
(1分)∴∠PAC=90º,∴tan∠APC=
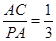 (1分)
(1分)设点Q(x,
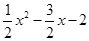 ),则QH=|
),则QH=|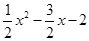 |,OH=|x-4| (1分)
|,OH=|x-4| (1分)∵∠BQH=∠APC,∴tan∠BQH=tan∠APC,∴
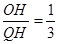
即
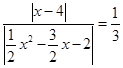 ,∴
,∴ 或
或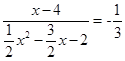 (1分)
(1分)解得
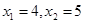 或
或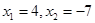 ,
,∴Q(4,0)(舍),Q(5,3)(舍),Q(-7,33)
∴Q(-7,33) (1分)
点评:熟知二次函数的一般式,顶点式,两点式的三种表现形式,本题由三个已知的点可用一般式即可,对于求三角函数值时,在初中阶段一定要有直角三角形,由已知得到各个边的长,从而求出函数值,(3)问需要注意的是根据等式解出三个答案要甄别是否符合题意,不符合的一定要舍去,这里容易出错,本题属于较难题型,问多,计算多,稍有疏忽就会做错,对概念定义,定理性质的要求较高。

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
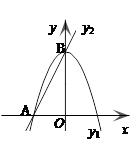
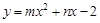 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.
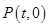 是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围. 与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形。
与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形。


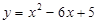 .
.  的形式;
的形式;  取何值时,
取何值时, 随
随 的图像经过点(-1,6)
的图像经过点(-1,6)