题目内容
【题目】如图,在正方形ABCD中,P是BC的中点,把△PAB沿着PA翻折得到△PAE,过C作CF⊥DE于F,若CF=2,则DF=_____.
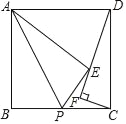
【答案】6.
【解析】
作辅助线,构建全等三角形,证明△AMD≌△DFC,则DM=FC=2,由折叠和正形
的边长相等得:AE=AD,根据等腰三角形三线合一得:DM=EM=2,∠EAM=∠MAD,设∠
MAD=α,则∠EAM=α,∠BAP=∠PAE=45°﹣α,可得∠PAM=45°,则△PAH是等腰直角三
角形,证明△PGE∽△AMD,列比例式得:GE=1,AM=2PG,设PG=x,则AM=2x,根据
AH=PH,得2x﹣1=2+x,求得x的值,即可解决问题;
过A作AM⊥DF于M,
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADF+∠FDC=90°,
∵∠ADF+∠MAD=90°,
∴∠FDC=∠MAD,
∵∠AMD=∠DFC=90°,
∴△AMD≌△DFC,
∴DM=FC=2,
由折叠得:AB=AE,BP=PE,
∵AB=AD,
∴AE=AD,
∴DM=EM=2,∠EAM=∠MAD,
∵P是BC的中点,
∴PC=![]() BC=
BC=![]() AD=PE,
AD=PE,
设∠MAD=α,则∠EAM=α,∠BAP=∠PAE=45°﹣α,
∴∠APE=90°﹣(45°﹣α)=45°+α,
∵∠EAM=∠DAM,∠BAP=∠PAE,
∴∠PAE+∠EAM=![]() ∠BAD=45°,
∠BAD=45°,
过P作PH⊥AM于H,过E作EG⊥PH于G,
∴△PAH是等腰直角三角形,
∴∠APH=45°,
∴∠HPE=α=∠MAD,
∵∠PGE=∠AMD=90°,
∴△PGE∽△AMD,
∴![]()
∴![]()
∴GE=1,AM=2PG,
设PG=x,则AM=2x,
∴AH=2x﹣1,
∵AH=PH,
∴2x﹣1=2+x,
x=3,
∴PG=3,AM=6,
∵△DAM≌△CDF,
∴DF=AM=6.
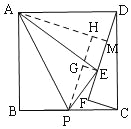
故答案为:6.

 名校课堂系列答案
名校课堂系列答案