题目内容
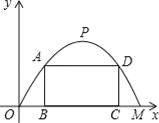
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左侧,
点在原点的左侧,![]() 点的坐标为
点的坐标为![]() ,与
,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
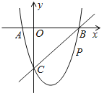
![]() 求这个二次函数的表达式.
求这个二次函数的表达式.
![]() 连接
连接![]() 、
、![]() ,并把
,并把![]() 沿
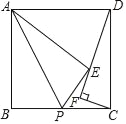
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 当点
当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
【答案】(1)![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() ,四边形
,四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.
【解析】
(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;
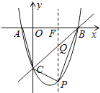
(3)由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
解:![]() 将
将![]() 、
、![]() 两点的坐标代入得
两点的坐标代入得![]() ,
,
解得:![]() ;
;
所以二次函数的表达式为:![]() ;
;
![]() 存在点
存在点![]() ,使四边形
,使四边形![]() 为菱形;
为菱形;
设![]() 点坐标为
点坐标为![]() ,
,![]() 交
交![]() 于
于![]()
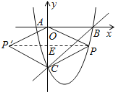
若四边形![]() 是菱形,则有
是菱形,则有![]() ;
;
连接![]() ,则
,则![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ;
;
∴![]()
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() 点的坐标为
点的坐标为![]()
![]() 过点
过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,设
,设![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
则![]() ,
,
解得:![]()
∴直线![]() 的解析式为
的解析式为![]() ,
,
则![]() 点的坐标为
点的坐标为![]() ;
;
当![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
当![]() 时,四边形
时,四边形![]() 的面积最大
的面积最大
此时![]() 点的坐标为
点的坐标为![]() ,四边形
,四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.

 春雨教育同步作文系列答案
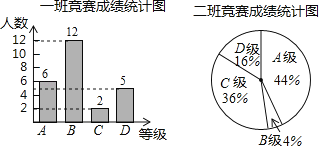
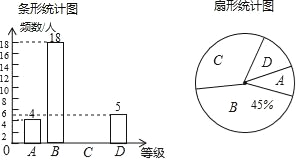
春雨教育同步作文系列答案【题目】在学校组织的八年级数学竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据提供的信息解答下列问题:
(1)此次竞赛中二班80分以上(包括80分)的人数为 ;
(2)请你将表格补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | 77.6 | 80 |
|
二班 | 77.6 |
| 90 |
(3)请从不同角度对这次竞赛成绩的结果进行分析.(至少两个角度)