��Ŀ����
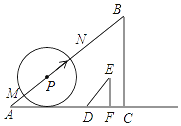
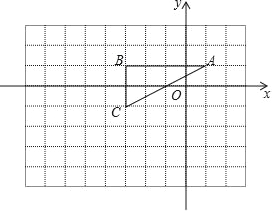
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ����һ��������Σ��������ε���������Ϊ��A��1��1����B����3��1����C����3����1����
��1������ABC�����Բ��Բ��ΪP�����P������Ϊ_____����P�İ뾶Ϊ_____��
��2����ͼ��ʾ����11��8������ͼ�ڣ�������ԭ��O��Ϊλ�����ģ�����ABC�����Ʊ�2��1�Ŵ�A��B��C�Ķ�Ӧ��ֱ�ΪA'��B'��C'���ٻ�����A'B'C'���ڽ���A'B'C'��x�᷽��ƽ�ƣ���ƽ��_____����λ���ȣ���ʹ��B'C'���ڵ�ֱ�����P���У�
���𰸡�����1��0�� ![]() 5��
5��![]() ��5+
��5+![]()
��������
��1���������֪��ABC��ֱ�������Σ��������Բ���ɣ�
��2������λ��ͼ�εĶ������������ͼ�Σ��ٸ���ƽ�ƵĶ�������ʼ����ߵ��ж����ɵ�ƽ�Ƶľ��룮
��1����ABC�����Բ��P��ͼ��ʾ
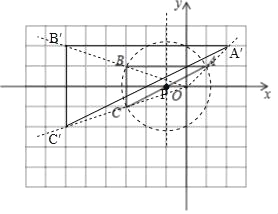
��ͼ��֪����P������Ϊ����1��0�����뾶Ϊ![]() =
=![]() ��
��
�ʴ�Ϊ������1��0����![]() ��
��
��2����ͼ��ʾ����A��B��C����Ϊ����
����A��B��C������ƽ��5��![]() ��5+
��5+![]() ����λB��C�����ڵ�ֱ�����P���У�
����λB��C�����ڵ�ֱ�����P���У�
�ʴ�Ϊ��5��![]() ��5+
��5+![]() ��
��

 �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
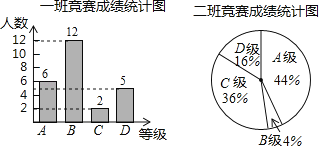
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�����Ŀ����ѧУ��֯�İ��꼶��ѧ�����У�ÿ��μӱ�����������ͬ���ɼ���ΪA��B��C��D�ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ90�֣�80�֣�70�֣�60�֣�ѧУ�����꼶һ��Ͷ���ijɼ����������Ƴ����µ�ͳ��ͼ��
��������ṩ����Ϣ����������⣺
��1���˴ξ����ж���80�����ϣ�����80�֣�������Ϊ�� ����
��2�����㽫����������
ƽ�������֣� | ��λ�����֣� | �������֣� | |
һ�� | 77.6 | 80 | �� �� |
���� | 77.6 | �� �� | 90 |
��3����Ӳ�ͬ�Ƕȶ���ξ����ɼ��Ľ�����з����������������Ƕȣ�
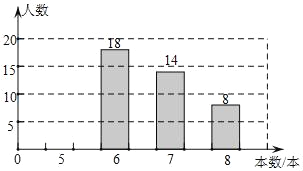
����Ŀ���������̨�����ʶ�������Ŀ������ͬѧ�ǵĶ������飬Ϊ������ѧ��������飬����������ijУ���꼶����ѧ���Ŀ����Ķ���������������飬�������������֣�ѧ�������Ķ��ı������ٵ���5����������8���������ݵ����������˲�������ͼ������ͼ��ʾ��
���������� | Ƶ���������� | Ƶ�� |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
�ϼ� | 50 | c |
���Ƕ���Ƶ��=![]() �������ɱ������ǿ���֪���������������г�������Ϊ50�˿����Ķ���Ϊ6����ͬѧΪ18�ˣ�������������Ӧ��Ƶ�ʾ���
�������ɱ������ǿ���֪���������������г�������Ϊ50�˿����Ķ���Ϊ6����ͬѧΪ18�ˣ�������������Ӧ��Ƶ�ʾ���![]() =0.36��
=0.36��
��1��ͳ�Ʊ��е�a��b��c��ֵ��
��2���뽫Ƶ���ֲ���ֱ��ͼ����������
��3�������б�����ѧ�������Ķ���ƽ��������
��4������У���꼶����600��ѧ��������Ϊ�������ϵ��������Թ��������У���꼶ѧ�������Ķ���Ϊ7����8����������Ϊ��������д����ļ�����̣�