题目内容
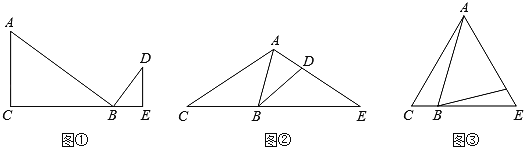
【题目】已知,点B在线段CE上.
(感知)(1)如图①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求证明);
(拓展)(2)如图②,△ACE中,AC=AE,且∠ABD=∠E,求证:△ACB∽△BED;
(应用)(3)如图③,△ACE为等边三角形,且∠ABD=60°,AC=6,BC=2,则△ABD与△BDE的面积比为 .
【答案】(1)见解析;(2)见解析;(3)7:2
【解析】
(1)由∠C=∠ABD=∠E=90°知∠A+∠ABC=∠ABC+∠DBE=90°,据此得∠A=∠DBE,从而得证.
(2)由∠C=∠ABD=∠E与∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,即可求得∠CAB=∠DBE,即可证得:△ACB∽△BED.
(3)由△ACB∽△BED,根据相似三角形的对应边成比例,可求得△ABC与△BDE的面积比,△ABC与△ABE的面积比,继而求得答案.
(1)∵∠C=∠ABD=∠E=90°,
∴∠A+∠ABC=∠ABC+∠DBE=90°,
∴∠A=∠DBE,
∴△ACB∽△BED;
(2)∵AC=AE,
∴∠C=∠E,
∵∠ABD=∠E,
∴∠C=∠ABD,
又∵∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,
∴∠CAB=∠DBE,
∴△ACB∽△BED;
(3)∵∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,∠C=∠ABD,
∴∠CAB=∠DBE,
∵∠C=∠E=60°,
∴△ACB∽△BED,△ACE是等边三角形,
∴AE=AC=6,
∴BE=CE﹣BC=4,
∴△ACB与△BED的相似比为:3:2,
∴S△ABC:S△BED=9:4,S△ABC:S△ABE=1:2=9:18,
设S△ABC=9x,则S△ABE=18x,S△BDE=4x,
∴S△ABD=S△ABE﹣S△BED=18x﹣4x=14x,
∴S△ABD:S△BDE=14:4=7:2.
故答案为:7:2.