Question

【题目】如图，⊙O中，直径CD⊥弦AB于M，AE⊥BD于E，交CD于N，连AC

（1）求证：AC＝AN；

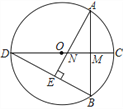
（2）若OM∶OC＝3∶5，AB＝5，求⊙O的半径；

Answer 1

【答案】（1）证明见解析（2）

【解析】试题分析：（1）连接AC，根据圆周角定理及直角三角形的性质得出∠BDC=∠EAB=∠BAC，再由ASA定理得出△AMN≌△AMC，进而可得出结论；

（2）连接OA，设OM=3x，OC=5x，根据勾股定理求出x的值，进而可得出结论．

试题解析：解：（1）连接AC，∵∠AED=∠AMO=90°，∴∠BDC=∠EAB=∠BAC．∵AM⊥OC，∴∠AMC=∠AMN．在△AMN与△AMC中，∵∠EAB=∠BAC，AM=AM，∠AMN=∠AMC，∴△AMN≌△AMC（ASA），∴AC=AN；

（2）连接OA，设OM=3x，OC=5x，∴OA=5x，AM=4x，∵AB=5，∴4x=，x=，∴r=5x=．