Question

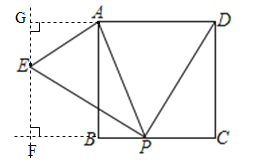
【题目】如图，正方形ABCD的边长为2，P为BC上一动点，将DP绕P逆时针旋转90°，得到PE，连接EA，则△PAE面积的最小值为__________．

Answer 1

【答案】

【解析】解：如图，过E作EF⊥CB于F，EG⊥DA于G．设BP=a，则PC=2-a，∵EP⊥PD，∴∠EPF+∠DPC=90°，∵∠DPC+∠PDC=90°，∴∠EPF=∠PDC．在△EPF和△PDC中，∵∠EPF=∠PDC，∠EFP=∠C=90°，EP=PD，∴△EPF≌△PDC，∴EF=PC=2-a，FP=DC=2，∴FB=2-a．∵∠AGF=∠GFB=∠ABF=90°，∴四边形GFBA是矩形，∴GA=FB=2-a，GF=AB=2，∴GE=a，∴△PAE的面积=梯形GFPA的面积－△AGE的面积－△EFP的面积

=（2-a+2）×2－×a(2-a)－×（2-a）×2= (a2-2a+4)= ，∵ ，∴当a=1时，△PAE的面积的最小值为．