Question

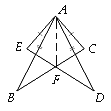
【题目】如图所示，为了改造小区环境，某小区决定要在一块一边靠墙（墙的最大可使用长度13 m）的空地上建造一个矩形绿化带．除靠墙一边（AD）外，用长为36 m的栅栏围成矩形ABCD，中间隔有一道栅栏（EF）．设绿化带宽AB为x m，面积为S m2

（1） 求S与x的函数关系式，并求出x的取值范围

（2） 绿化带的面积能达到108 m2吗？若能，请求出AB的长度；若不能，请说明理由

（3） 当x为何值时，满足条件的绿化带面积最大

Answer 1

【答案】（1）S=-3x2+36x（≤x<12）（2）不能 （3）

【解析】试题分析：（1）首先根据矩形的性质，由绿化带的AB边长为x（m），可得BC=36-3x ，然后根据矩形面积的求解方法，即可求得y与x之间的函数关系式，又由墙的最大可使用长度13 m，即可求得自变量的x的范围．

(2)令y=108解方程后判断即可；

（3）根据（1）中的二次函数的增减性，可知当x＞6时，y随x的增大而减小，故可得当x=时，y最大，从而得到结论．

试题解析：解：（1）∵四边形ABCD是矩形，∴AB=CD=EF，AD=BC，∵AB=xm，AB+BC+CD+EF=36m，∴BC=36-3x，∴绿化带的面积为：y=x（36-3x）=﹣3x2+36x，由，解得： ，∴y与x之间的函数关系式为：y=﹣3x2+36x（）；

（2）由题意得：﹣3x2+36x=108，解得：x1=x2=6，∵6＜，∴绿化带的面积不能达到108 m2．

（3）∵y=﹣3x2+36x =﹣3（x﹣6）2+108，∵a=﹣3＜0，∴当x＞6时，y随x的增大而减小，∴当x=时，y最大，∴当x取时绿化带的面积最大．