Question

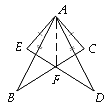
【题目】如图 1，直线 m 与直线 n 垂直相交于点 O ，点 A 在直线 m 上运动，点 B 在直线 n 上运动， AC 、 BC 分别是BAO 和ABO 的角平分线.

（1）求ACB 的大小；

（2）如 图 2，若 BD 是AOB 的外角OBE 的角平分线，BD 与 AC 相交于点 D ，点 A 、B 在运动的过程中，ADB的大小是否会发生变化？若发生变化，请说明理由，若不发生变化，试求出其值.

Answer 1

【答案】（1）135°，（2）45°.

【解析】

（1）根据三角形的内角和得到∠OAB+∠OBA=90°，再根据AC 、 BC 分别是BAO 和ABO 的角平分线得到∠CAB+∠CBA=45°，再利用三角形的内角和即可求解∠ACB的度数；

（2）根据BC是ABO 的角平分线，BD是OBE 的角平分线得到∠DBC=90°，由（1）得到∠BCD=45°，故可求出∠ADB的度数.

（1）AO⊥BO，∴∠OAB+∠OBA=90°

∵AC 、 BC 分别是BAO 和ABO 的角平分线

∴∠CAB+∠CBA=∠OAB +∠OBA =（∠OAB+∠OBA）=45°

∴∠ACB=180°-（∠CAB+∠CBA）=135°，

（2）不变，∠ADB=45°，

理由如下：

∵BC是ABO 的角平分线，BD是OBE 的角平分线

∴∠DBC=∠DBG+∠GBC=∠EBG +∠OBA=(∠EBG+∠OBA)=90°，

又∠BCD=180°-ACB =45°

∴∠ADB=180°-∠DBC-∠BCD=45°.