题目内容
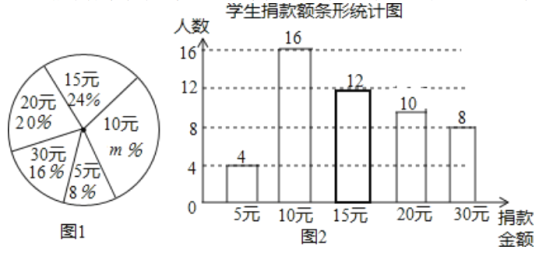
【题目】某校学生会向全校2400名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答系列问题:
(1)本次接受随机抽样调查的学生人数为 人,图1中m的值是 ;
(2)求本次调查获取的样本数据的平均数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
【答案】(1)50,32;(2)16,15;(3)768.
【解析】
(1)根据题意由5元的人数及其所占百分比可得抽样调查的学生人数,用10元人数除以抽样调查的学生人数可得m的值;
(2)由题意根据统计图可以分别得到本次调查获取的样本数据的平均数和中位数;
(3)由题意根据全校总人数捐款金额为10元的学生人数所占乘以抽样调查的学生人数的比例,即可估计该校本次活动捐款金额为10元的学生人数.
解:(1)本次接受随机抽样调查的学生人数为4÷8%=50人,
∵![]() ,
,
![]() .
.
故答案为:50;32.
(2)本次调查获取的样本数据的平均数是:![]() (元);
(元);
本次调查获取的样本数据的中位数是:15元.
(3)估计该校本次活动捐款金额为10元的学生人数为2400×32%=768人.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1