题目内容
【题目】在新修的花园小区中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB、BC、CD三段绿色长廊上各修建一凉亭E、M、F,且BE=CF,M是BC的中点,E、M、F在一条直线上.若在凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能知道M与F之间的距离吗?试说明理由.
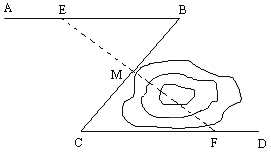
【答案】测出EM 的距离就知道了M与F之间的距离, 理由见解析.
【解析】
由AB∥CD 根据平行线的性质得 ∠B =∠C , ∠BEM=∠CFM ,由M是BC的中点得BM=MC,根据“AAS”即可证得三角形EBM与三角形FCM全等,因此ME=MF.
测出ME的距离就知道了M与F之间的距离.
理由如下:∵AB∥CD,
∴∠B=∠C,∠BEM=∠CFM,
∵M是BC的中点,
∴BM=MC,
在△EBM和△FCM中,
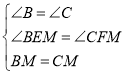 ,
,
∴△EBM≌△FCM(AAS),
∴ME=MF.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1