题目内容
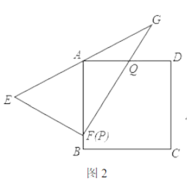
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 为靠近点
为靠近点![]() 的四等分点,点
的四等分点,点![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() 连接
连接![]() 则点
则点![]() 到
到![]() 所在直线距离为________________.
所在直线距离为________________.
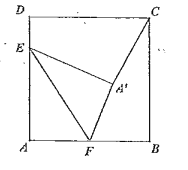
【答案】![]()
【解析】
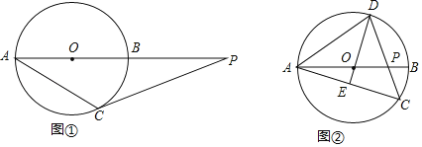
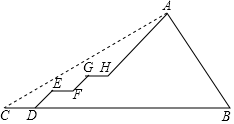
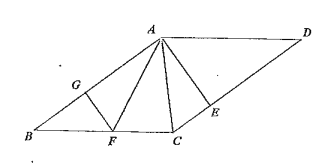
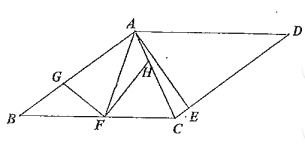
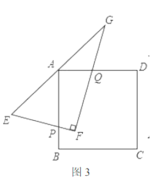
延长![]() 交BC于点M,连接FM,延长
交BC于点M,连接FM,延长![]() 交DA的延长线于点P,作DN⊥CP,先证明
交DA的延长线于点P,作DN⊥CP,先证明![]() ∽
∽![]() ,利用相似的性质求出
,利用相似的性质求出![]() ,然后证明
,然后证明![]() ∽
∽![]() ,利用相似的性质求出EP,从而得到DP的长,再利用勾股定理求出CP的长,最后利用等面积法计算DN即可.
,利用相似的性质求出EP,从而得到DP的长,再利用勾股定理求出CP的长,最后利用等面积法计算DN即可.
如图,延长![]() 交BC于点M,连接FM,延长
交BC于点M,连接FM,延长![]() 交DA的延长线于点P,作DN⊥CP,
交DA的延长线于点P,作DN⊥CP,

由题可得,![]() ,
,![]() ,
,
∴![]() ,
,
∵F为AB中点,
∴![]() ,
,
又∵FM=FM,
∴![]() ≌
≌![]() (HL),
(HL),
∴![]() ,
,![]() ,
,
由折叠可知,![]() ,
,
∴![]() ,
,
又∵![]()
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵AD=4,E为四等分点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即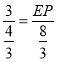 ,
,
∴EP=6,
∴DP=EP+DE=7,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
【题目】行驶中的汽车,在刹车后由于惯性的原因,还要继续向前滑行一段距离才能停住,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能,对这种汽车的刹车距离进行测试,测得的数据如下表:
刹车时车速(千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
刹车距离(米) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.6 | 2.1 |
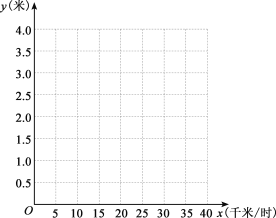
(1)在如图所示的直角坐标系中,以刹车时车速为横坐标,以刹车距离为纵坐标,描出这些数据所表示的点,并用平滑的曲线连结这些点,得到某函数的大致图象;
(2)测量必然存在误差,通过观察图象估计函数的类型,求出一个大致满足这些数据的函数表达式;
(3)一辆该型号汽车在高速公路上发生交通事故,现场测得刹车距离约为40米,已知这条高速公路限速100千米/时,请根据你确定的函数表达式,通过计算判断在事故发生时,汽车是否超速行驶.