题目内容
【题目】在平行四边形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,点
,点![]() 分别为
分别为![]() 边上的点,连接
边上的点,连接![]() 平分
平分![]() .
.
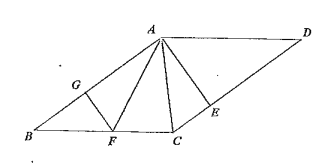
(1)如图,若![]() 且
且![]() ,求平行四边形
,求平行四边形![]() 的面积.
的面积.
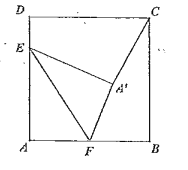
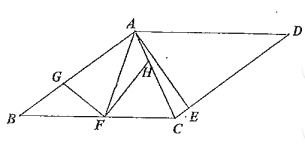
(2)如图,若![]() 过
过![]() 作
作![]() 交
交![]() 于
于![]() 求证:
求证:![]()
【答案】(1)50;(2)详见解析
【解析】
(1)过点A作AH⊥BC,根据角平分线的性质可求出AH的长度,再根据平行四边形的性质与∠B的正弦值可求出AD,最后利用面积公式即可求解;
(2)截取FM=FG,过F作FN⊥AF交AC延长线于点N,利用SAS证明![]() ≌
≌![]() ,根据全等的性质、各角之间的关系及平行四边形的性质可证明
,根据全等的性质、各角之间的关系及平行四边形的性质可证明![]() ,从而得到
,从而得到![]() 为等腰直角三角形,再利用ASA证明
为等腰直角三角形,再利用ASA证明![]() 与
与![]() 全等,最后根据全等的性质即可证明结论.
全等,最后根据全等的性质即可证明结论.
解:(1)过![]() 作
作![]() ,
,
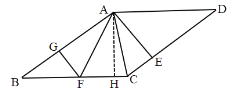
∵![]() 平分
平分![]() 且
且![]() ,
,
∴![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴∠B=∠D,
∴sinB=sinD=![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)在![]() 上截取
上截取![]() ,过
,过![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,
,
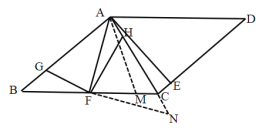
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,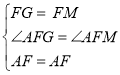 ,
,
∴![]() ≌
≌![]() (SAS),
(SAS),
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵平行四边形![]() 中:
中:![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 为等腰直角三角形,
为等腰直角三角形,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,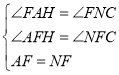 ,
,
∴![]() ≌
≌![]() (ASA),
(ASA),
∴![]() ,
,
∵在![]() 中,
中,![]() ,即
,即![]() ,
,
∴![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目