题目内容
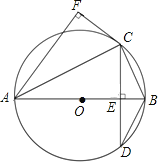
【题目】如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且cosB=![]() .
.
(1)求AB的长度;
(2)求ADAE的值;
(3)过A点作AH⊥BD,求证:BH=CD+DH.

【答案】(1)AB=![]() ;(2)ADAE =10;(3)见解析.
;(2)ADAE =10;(3)见解析.
【解析】
(1)作AM垂直于BC,由AB=AC,利用三线合一得到CM等于BC的一半,求出CM的长,再由cosB的值,利用锐角三角函数定义求出AB的长即可;
(2)连接DC,由等边对等角得到一对角相等,再由圆内接四边形的性质得到一对角相等,根据一对公共角,得到三角形EAC与三角形CAD相似,由相似得比例求出所求即可;
(3)在BD上取一点N,使得BN=CD,利用SAS得到三角形ACD与三角形ABN全等,由全等三角形对应边相等及等量代换即可得证.
(1)作AM⊥BC,
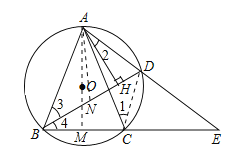
∵AB=AC,AM⊥BC,BC=2BM,
∴CM=![]() BC=1,
BC=1,
∵cosB=![]() ,
,
在Rt△AMB中,BM=1,
∴AB=![]() ;
;
(2)连接DC,
∵AB=AC,
∴∠ACB=∠ABC,
∵四边形ABCD内接于圆O,
∴∠ADC+∠ABC=180°,
∵∠ACE+∠ACB=180°,
∴∠ADC=∠ACE,
∵∠CAE公共角,
∴△EAC∽△CAD,
∴![]() ,
,
∴ADAE=AC2=10;
(3)在BD上取一点N,使得BN=CD,
在△ABN和△ACD中 AB=AC,∠3=∠1,BN=CD,
∴△ABN≌△ACD(SAS),
∴AN=AD,
∵AN=AD,AH⊥BD,
∴NH=HD,
∵BN=CD,NH=HD,
∴BN+NH=CD+HD=BH.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目