题目内容
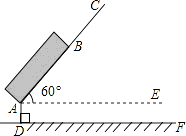
【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示，箱体长AB=50cm，拉杆最大伸长距离BC=30cm，点A到地面的距离AD=8cm，旅行箱与水平面AE成60°角，求拉杆把手处C到地面的距离（精确到1cm）．（参考数据： 
）
【答案】解：作CG⊥AE于点G．
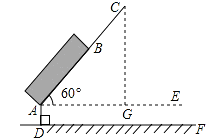
在直角△ACG中，AC=AB+BC=50+30=80cm．
sin∠CAG= 
，
∴CG=ACsin∠CAG=80× 
=40 
≈69．2（cm）．
则拉杆把手处C到地面的距离是：69．2+8=77．2≈77cm
【解析】将所要解决的问题转化到直角三角形中，因此作CG⊥AE于点G．在Rt△AGC中，利用解直角三角形求出CG的长即可。
【考点精析】掌握解直角三角形是解答本题的根本，需要知道解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
练习册系列答案
相关题目
