题目内容
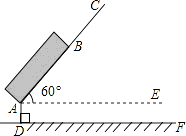
【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )

A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
【答案】D
【解析】
直接利用平行线的性质结合翻折变换的性质得出△ADM≌△BCM(SAS),进而利用直角三角形的性质得出答案.
∵M为CD中点,
∴DM=CM,
在△ADM和△BCM中
∵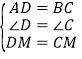 ,
,
∴△ADM≌△BCM(SAS),
∴∠AMD=∠BMC,AM=BM
∴∠MAB=∠MBA
∵将点C绕着BM翻折到点E处,
∴∠EBM=∠CBM,∠BME=∠BMC=∠AMD
∴∠DME=∠AMB
∴∠EBM=∠CBM=![]() (90°-β)
(90°-β)
∴∠MBA=![]() (90°-β)+ β=
(90°-β)+ β=![]() (90°+β)
(90°+β)
∴∠MAB=∠MBA=![]() (90°+β)
(90°+β)
∴∠DME=∠AMB=180°-∠MAB-∠MBA=90°-β
∵长方形ABCD中,
∴CD∥AB
∴∠DMA=∠MAB=![]() (90°+β)
(90°+β)
∴∠DME+∠AME=∠ABE+∠MBE
∵∠AME=α,∠ABE=β,
∴90°-β+α=β+![]() (90°-β)
(90°-β)
∴3β-2α=90°
故选:D.

练习册系列答案
相关题目