��Ŀ����
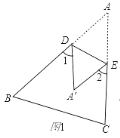
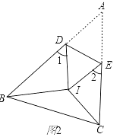
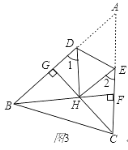
����Ŀ����ͼ1��E�ǵȱ�������ABC�ı�AB����ֱ����һ�㣬D�DZ�BC����ֱ����һ�㣬��D��C���غϣ���EC��ED�����DΪ��C���ڵȱ�������ABC�ķ��Ƶ㣬��E��Ϊ�������ģ�
��ƽ��ֱ������ϵxOy�У�
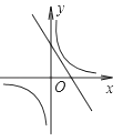
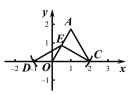
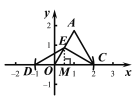
��1����֪�ȱ�������AOC�Ķ���C������Ϊ��2��0������A�ڵ�һ�����ڣ���������E��ֱ��AO�ϣ����Ƶ�D��ֱ��OC�ϣ�
����ͼ2����EΪ��AO���е㣬��ͼ��������C���ڵȱ�������AOC�ķ��Ƶ�D����ֱ��д����D�����꣺�� ����
����AE��2�����C���ڵȱ�������AOC�ķ��Ƶ�D�����ꣻ
��2�����ȱ�������ABC�Ķ���ΪB��n��0����C��n+1��0������������E��ֱ��AB�ϣ����Ƶ�D��ֱ��BC�ϣ���2��AE��3����ֱ��д����C���ڵȱ�������ABC�ķ��Ƶ�D�ĺ�����t��ȡֵ��Χ���� �����ú�n�Ĵ���ʽ��ʾ����

���𰸡�(1)��D��-1,0��; ��D(![]() 2,0);(2)
2,0);(2) ![]() ��
��![]()
��������
��1���ٸ������з��Ƶ��뷴�����ĵĶ���������D���ɵ����ꣻ
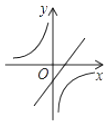
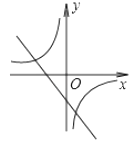
����AO=OC=2����AE=2,��E����������ܵ�λ�ã���ͼ3��ͼ4�����ۣ��ɵ�D���ֵ��
(2)�ɣ�1���ɵ÷��Ƶ��뷴�����ĵĹ��ɣ���B(n,0)��C(n+1,0)��2��AE<3�ɵ�![]() ��
��![]() .
.
��1���� ��ͼ��
 ��
�� 
D(-1,0)
�� �ߵȱ�������AOC����������ΪO(0,0)��C(2,0),
��OC=2.
��AO=OC=2.
��AE=2��֪����E���������ܵ�λ�ã���ͼ3��ͼ4��.
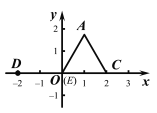

ͼ3 ͼ4
(��) ��ͼ3����E������ԭ��O�غ�.
��EC=ED��EC=2,
��ED=2.
��D�DZ�OC����ֱ����һ�㣬��D��C���غ�,
��D������Ϊ(![]() 2,0) .
2,0) .
(��) ��ͼ4����E�ڱ�OA���ӳ����ϣ���AE=2.
��AC=AE=2,
���E=��ACE.
�ߡ�AOCΪ�ȱ�������,
���OAC =��ACO=60��.
���E=��ACE=30��.
���OCE=90��.
��EC=ED,
���D���C�غ�.
������Ŀ�����е�D��C���غ�ì�ܣ�����ͼ4�е����������Ҫ����ȥ.
����������D(![]() 2,0). ��
2,0). ��
��2��![]() ��
��![]() .
.