题目内容
【题目】阅读下列材料:
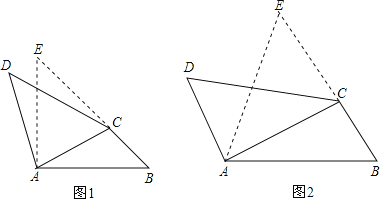
如图,在四边形 ABCD 中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,

求证:CD=AB
小刚是这样思考的;由已知可得,∠CAB=30°,∠DAC=75°,∠DCA=60°,∠ACB+∠DAC=180°,由求证及特殊度数可联想到构造特殊三角形,即过点 A 作 AE⊥AB 交 BC 的延长线于点 E,对 AB=AE,∠E=∠D
在△ADC 与△CEA 中,
∠D = ∠E,∠DAC = ∠ECA = 75° ,AC = CA.
△ADC≌△CEA.
得 CD=AE=AB
请你参考小刚同学思考问题的方法,解决下面问题
如图,在四边形 ABCD 中,若∠ACB+∠CAD=180°,∠B=∠D,请问:CD 与 AB 否相等?若相等,请你给出证明;若不相等。请说明理由.

【答案】CD=AB. 证明见解析;
【解析】
作AE=AB交BC延长线于E点,则∠B=∠E,而∠B=∠D,得到∠D=∠E,由∠ACB+∠DAC=180°,∠ACB+∠ECA=180°可得到∠DAC=∠ECA,然后根据“AAS”可判断△DAC≌△ECA,根据全等的性质得CD=AE,于是有CD=AB.
CD=AB.
证明如下:作AE=AB交BC延长线于E点,
∴∠B=∠E
∵∠B=∠D
∴∠D=∠E,
∵∠ACB+∠DAC=180°,∠ACB+∠ECA=180°,
∴∠DAC=∠ECA,
∵在△DAC和△ECA中,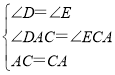 ,
,
∴△DAC≌△ECA(AAS),
∴CD=AE
∴CD=AB.

练习册系列答案
相关题目