题目内容
【题目】如图，已知四边形ABCD是边长为3的正方形，动点P从点B出发，沿BC向终点C运动，点P可以与点B、点C重合，连接PD，将
沿直线PD折叠，设折叠后点C的对应点为点E，连接AE并延长交BC于点F，连接BE，则下列结论中：
当
时，
为等边三角形；
当时，F为BC的中点；
当
时，
；
当点P从点B运动到点C时，点E所走过的路径的长为
其中正确的有
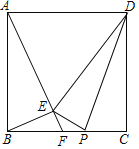
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据题意可得
为等边三角形，因此可判断
，由E点所走过的路径是以D为圆心，CD为半径的
圆可判断
由沿直线PD折叠得到
可得CE的长，根据相似可得EM，BM的长，以B点为原点，BC为x轴，AB为y轴建立直角坐标系，可求AE，BE解析式，根据
，两直线垂直，可判断
．
解：
且将
沿直线PD折叠得到
，
，
即
且
为等边三角形
，
且
故
正确，
错误
是定值3，
点E所走过的路径是以D为圆心，DC长为半径的圆
点E所走过的路径
故
正确
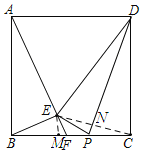
连接EC交DP于N，作
，
由勾股定理得：
将沿直线PD折叠得到
，
，
，
∽
，
以B点为原点，BC为x轴，AB为y轴建立直角坐标系
，
可得BE解析式
，
AE解析式
故正确
故选：C．
练习册系列答案
相关题目
