题目内容
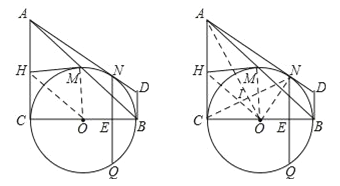
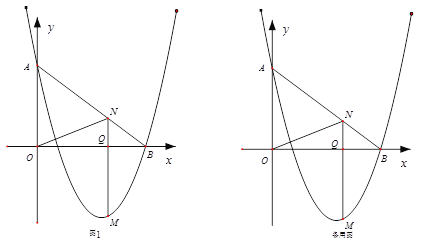
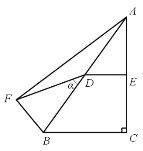
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.
(1)求证:MH为⊙O的切线.
(2)若MH=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求⊙O的半径.
,求⊙O的半径.
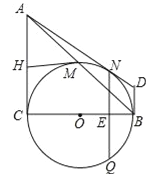
(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.
【答案】(1)证明见解析;(2)2;(3)![]() .
.
【解析】
(1)连接OH、OM,易证OH是△ABC的中位线,利用中位线的性质可证明△COH≌△MOH,所以∠HCO=∠HMO=90°,从而可知MH是⊙O的切线;
(2)由切线长定理可知:MH=HC,再由点M是AC的中点可知AC=3,由tan∠ABC=![]() ,所以BC=4,从而可知⊙O的半径为2;
,所以BC=4,从而可知⊙O的半径为2;
(3)连接CN,AO,CN与AO相交于I,由AC、AN是⊙O的切线可知AO⊥CN,利用等面积可求出可求得CI的长度,设CE为x,然后利用勾股定理可求得CE的长度,利用垂径定理即可求得NQ.
解:(1)连接OH、OM,∵H是AC的中点,O是BC的中点
∴OH是△ABC的中位线
∴OH∥AB,∴∠COH=∠ABC,∠MOH=∠OMB
又∵OB=OM,∴∠OMB=∠MBO
∴∠COH=∠MOH,
在△COH与△MOH中,
∵OC=OM,∠COH=∠MOH,OH=OH
∴△COH≌△MOH(SAS)
∴∠HCO=∠HMO=90°
∴MH是⊙O的切线;
(2)∵MH、AC是⊙O的切线
∴HC=MH=![]()
∴AC=2HC=3
∵tan∠ABC=![]() ,∴
,∴![]() =
=![]()
∴BC=4
∴⊙O的半径为2;
(3)连接OA、CN、ON,OA与CN相交于点I
∵AC与AN都是⊙O的切线
∴AC=AN,AO平分∠CAD
∴AO⊥CN
∵AC=3,OC=2
∴由勾股定理可求得:AO=![]()
∵![]() ACOC=
ACOC=![]() AOCI,∴CI=
AOCI,∴CI=![]()
∴由垂径定理可求得:CN=![]()
设OE=x,由勾股定理可得:
![]()
∴![]() ,
,
∴x=![]() ,∴CE=
,∴CE=![]() ,
,
由勾股定理可求得:EN=![]() ,
,
∴由垂径定理可知:NQ=2EN=![]() .
.