题目内容
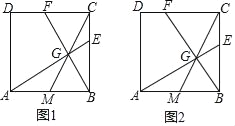
【题目】已知正方形ABCD,点M为边AB的中点.
(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BCCE.
(2)如图2,在边BC上取一点E,满足BE2=BCCE,连接AE交CM于点G,连接BG并延长交CD于点F,求tan∠CBF的值.
【答案】(1)①证明见解析;②证明见解析;(2)![]() .
.
【解析】【试题分析】
(1)①在正方形ABCD中,AB=BC,∠ABC=∠BCF=90°,
因为∠ABG+∠CBF=90°,∠ABG+∠BAG=90°,根据同角的余角相等,得∠BAG=∠CBF,利用ASA判定定理得△ABE≌△BCF,根据全等三角形的对应边相等得:BE=CF.
②∠AGB=90°,点M为AB的中点,直角三角形斜边上的中线等于斜边的一半,得,MG=MA=MB,根据等边对等角得∠GAM=∠AGM.
因为∠CGE=∠AGM,等量代换得∠GAM=∠CGE.
由①可知∠GAM=∠CBG,则∠CGE=∠CBG.
又因为∠ECG=∠GCB,根据两角对应相等,两三角形相似得:△CGE∽△CBG,根据相似三角形对应边成比例得:![]() ,即CG2=BC·CE.∵MG=MB,∴∠MGB=∠MBG.
,即CG2=BC·CE.∵MG=MB,∴∠MGB=∠MBG.
在正方形ABCD中,因为AB∥CD,根据平行线的性质得∠MBG=∠CFG.
又因为∠CGF=∠MGB,等量代换得∠CFG=∠CGF,根据等边对等角得CF=CG.
由①可知BE=CF,即BE=CG,故BE2=BC·CE.
(2)延长AE,DC交于点N.在正方形ABCD中, AB=BC,AB∥CD,∴△CEN∽△BEA,根据相似三角形的对应边成比例得![]() ,即BE·CN=AB·CE.因为AB=BC,
,即BE·CN=AB·CE.因为AB=BC,
则BE2=BC·CE,得CN=BE.由于AB∥DN,得△CGN∽△MGA,△CGF∽△MGB,
则 ![]() ,
,![]() ,∴
,∴![]() . 又因为点M为AB的中点,得MA=MB,
. 又因为点M为AB的中点,得MA=MB,
则CN=CF=BE.
设正方形的边长为a,BE=x,则CE=BC-BE=a-x.由BE2=BC·CE列方程得:x2=a·(a-x),解得x1=![]() a,x2=
a,x2=![]() a(舍去),
a(舍去),![]() =
=![]() ,即tan∠CBF=
,即tan∠CBF=![]() =
=![]() =
=![]() .
.
【试题解析】
(1)①∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠BCF=90°,∴∠ABG+∠CBF=90°.∵∠AGB=90°,∴∠ABG+∠BAG=90°,∴∠BAG=∠CBF,∴△ABE≌△BCF,∴BE=CF.
②∵∠AGB=90°,点M为AB的中点,∴MG=MA=MB,∴∠GAM=∠AGM.
∵∠CGE=∠AGM,∴∠GAM=∠CGE.
由①可知∠GAM=∠CBG,∴∠CGE=∠CBG.
又∵∠ECG=∠GCB,∴△CGE∽△CBG,∴![]() ,
,
即CG2=BC·CE.∵MG=MB,∴∠MGB=∠MBG.
∵四边形ABCD是正方形,∴AB∥CD,∴∠MBG=∠CFG.
又∵∠CGF=∠MGB,∴∠CFG=∠CGF,∴CF=CG.
由①可知BE=CF,∴BE=CG,∴BE2=BC·CE.
(2)延长AE,DC交于点N.∵四边形ABCD是正方形,∴AB=BC,AB∥CD,∴△CEN∽△BEA,∴![]() ,即BE·CN=AB·CE.∵AB=BC,BE2=BC·CE,∴CN=BE.∵AB∥DN,∴△CGN∽△MGA,△CGF∽△MGB,∴
,即BE·CN=AB·CE.∵AB=BC,BE2=BC·CE,∴CN=BE.∵AB∥DN,∴△CGN∽△MGA,△CGF∽△MGB,∴ ![]() ,
,![]() ,∴
,∴![]() . ∵点M为AB的中点,∴MA=MB,∴CN=CF,∴CF=BE.
. ∵点M为AB的中点,∴MA=MB,∴CN=CF,∴CF=BE.
设正方形的边长为a,BE=x,则CE=BC-BE=a-x.由BE2=BC·CE可得x2=a·(a-x),解得x1=![]() a,x2=
a,x2=![]() a(舍去),∴
a(舍去),∴![]() =
=![]() ,∴tan∠CBF=
,∴tan∠CBF=![]() =
=![]() =
=![]() .
.