题目内容
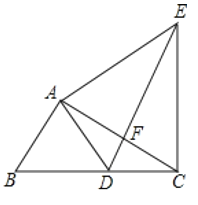
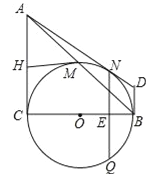
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交CE于点G,连结BE. 下列结论中:① CE=BD; ②△ADC是等腰直角三角形;
③∠ADB=∠AEB; ④ CD·AE=EF·CG;
一定正确的结论有
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
∴故①正确;
②∵四边形ACDE是平行四边形,
∴∠EAD=∠ADC=90°,AE=CD,
∵△ADE都是等腰直角三角形,
∴AE=AD,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴②正确;
③∵△ADC是等腰直角三角形,
∴∠CAD=45°,
∴∠BAD=90°+45°=135°,
∵∠EAD=∠BAC=90°,∠CAD=45°,
∴∠BAE=360°-90°-90°-45°=135°,又AB=AB,AD=AE,
∴△BAE≌△BAD(SAS),
∴∠ADB=∠AEB;故③正确;
④∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠AEC=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,
∴∠GDF+GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴![]() ,
,
∴CDAE=EFCG.故④正确,故正确的有4个.
故选D.

练习册系列答案
相关题目