题目内容
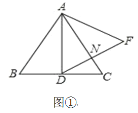
【题目】如图,![]() 是
是![]() 中
中![]() 边上的中线,过点
边上的中线,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 为
为![]() 外一点,连接
外一点,连接![]() ,且
,且![]() .求证:
.求证:
(1)![]() ;
;
(2)CA平分![]() .
.
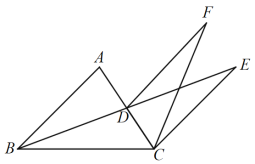
【答案】(1)见解析;(2)见解析
【解析】
(1)根据中线得AD=DC,根据平行线得∠A=∠DCE,∠ABD=∠E,进而根据“AAS”即可得证;
(2)由(1)可得BD=DE,结合DE=DF可得BD=DF,根据等角的补角相等可得∠CDF=∠CDB,进而根据“SAS”可得△CDF≌△CDB,进而得到∠DCF=∠DCB即可得证.
证明:(1)∵BD是△ABC的中线,
∴AD=DC,
∵CE∥AB,
∴∠A=∠DCE,∠ABD=∠E,
在△ABD与△CED中,
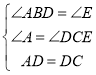
∴△ABD≌△CED(AAS),
(2)∵△ABD≌△CED,
∴BD=DE,
∵DE=DF,
∴BD=DF,
∵∠ADF=∠CDE,∠ADF+∠CDF=180°,∠CDE+∠CDB=180°,
∴∠CDF=∠CDB,
在△CDF与△CDB中,
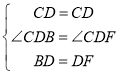
∴△CDF≌△CDB(AAS),
∴∠DCF=∠DCB,
∴CA平分∠BCF.

练习册系列答案
相关题目
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.