题目内容
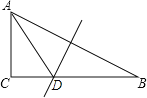
【题目】如图，在□ABCD中，CE
AD于点E，且CB=CE，点F为CD边上的一点，CB=CF，连接BF交CE于点G.
（1）若
，CF=
，求CG的长；
（2）求证：AB=ED+CG
【答案】（1）CG=2；（2）证明见解析.
【解析】
（1）根据平行四边形的性质得到AD//BC，然后得到∠GBC=30°，利用tan∠GBC=
=
=
,求得GC=2；
（2）延长EC到点H，连接BH，证得△HBC≌△DCE，根据各角之间的关系得到∠4=∠GBH，从而得到BH=GH，证得DC=ED+CG．
四边形ABCD是平行四边形，
AD//BC，
CE
AD，
，
，
，
BC=CF
，
在Rt
BCG中，
，
，
GC=2
（2）延长
到点
，使得
，连接BH ，
，
，
，
，
，
，
，
，
，
【题目】我市启动了第二届“美丽港城，美在阅读”全民阅读活动，为了解市民每天的阅读时间情况，随机抽取了部分市民进行调查，根据调查结果绘制如下尚不完整的频数分布表：
阅读时间 | 0≤x＜30 | 30≤x＜60 | 60≤x＜90 | x≥90 | 合计 |
频数 | 450 | 400 | 50 | ||
频率 | 0.4 | 0.1 | 1 |
（1）补全表格；
（2）将每天阅读时间不低于60min的市民称为“阅读爱好者”，若我市约有500万人，请估计我市能称为“阅读爱好者”的市民约有多少万人？
【题目】某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5～60.5 | 2 | a |
2 | 60.5～70.5 | 6 | 0.15 |
3 | 70.5～80.5 | b | c |
4 | 80.5～90.5 | 12 | 0.30 |
5 | 90.5～100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |
（1）表中a= ， b= ， c=；
（2）请补全频数分布直方图；
（3）该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数． 
