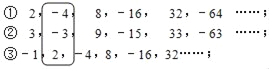题目内容
【题目】我们知道1+2+3+…+![]() =
=![]() ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .
[问题提出] 那么 ![]() 的结果等于多少呢?
的结果等于多少呢?
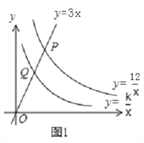
[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+![]() n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
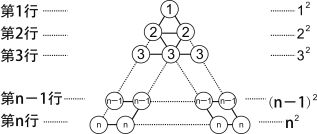
图1
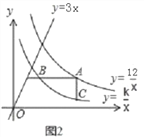
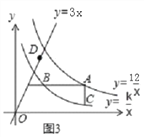
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(![]() )=_________________.因此,
)=_________________.因此,![]() =__________.
=__________.

图2
[问题解决]
(1).根据以上规律可得![]() __________________.
__________________.
(2).试计算 ![]() ,请写出计算步骤.
,请写出计算步骤.
【答案】55;![]() ;
;![]() ;(
;(![]() );
);![]() ;
;![]() ;(1)7;(2)2485
;(1)7;(2)2485
【解析】
把n=10代入1+2+3+…+![]() =
=![]() ,即可求出1+2+3+…+10的值;
,即可求出1+2+3+…+10的值;
[阅读理解]:由图1可知,共有1+2+3+…+n=![]() 个圆圈,所有圆圈中数的和可表示为
个圆圈,所有圆圈中数的和可表示为![]() ;
;
[规律探究]:由图2知,每个位置上三个圆圈中的数的和均为![]() .由此可得,这三个三角形数阵所有圆圈中数的总和为:3(
.由此可得,这三个三角形数阵所有圆圈中数的总和为:3(![]() )=每个位置上三个圆圈中的数的和(
)=每个位置上三个圆圈中的数的和(![]() )×位置的个数
)×位置的个数![]() ,因此,
,因此,![]() =
=![]() ;
;
[问题解决]:(1)先化简把![]() ,然后把n=10代入就算即可;(2)用(
,然后把n=10代入就算即可;(2)用(![]() )减去(
)减去(![]() )即可求出结论.
)即可求出结论.
当n=10时,
1+2+3+…+![]() =
=![]() =55;
=55;
[阅读理解]:由图1可知,共有1+2+3+…+n=![]() 个圆圈,所有圆圈中数的和可表示为
个圆圈,所有圆圈中数的和可表示为![]() ;
;
[规律探究]:由图2知,每个位置上三个圆圈中的数的和均为![]() .由此可得,这三个三角形数阵所有圆圈中数的总和为:3(
.由此可得,这三个三角形数阵所有圆圈中数的总和为:3(![]() )=
)=![]() ,因此,
,因此,![]() =
=![]() ;
;
[问题解决]:(1)∵![]() ,
,
把n=10代入得,
原式=![]() =7;
=7;
(2)![]()
=(![]() )-(
)-(![]() )
)
=![]()
=![]()
=2485.

【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
【题目】![]() 两地盛产柑桔,
两地盛产柑桔,![]() 地有柑桔200吨,
地有柑桔200吨,![]() 地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知
地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知![]() 仓库可储存240吨,
仓库可储存240吨,![]() 仓库可储存260吨;从
仓库可储存260吨;从![]() 地运往C、D两处的费用分别为每吨20元和25元,从
地运往C、D两处的费用分别为每吨20元和25元,从![]() 地运往C、D两处的费用分别为每吨15元和18元.设从
地运往C、D两处的费用分别为每吨15元和18元.设从![]() 地运往
地运往![]() 仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
(1)请填写下表后分别求出yA,yB之间的函数关系式,并写出定义域;
| C | D | 总计 |
A | x吨 | 200吨 | |
B | 300吨 | ||
总计 | 240吨 | 260吨 | 500吨 |
(2)试讨论A,B两地中,哪个运费较少;