题目内容
【题目】在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.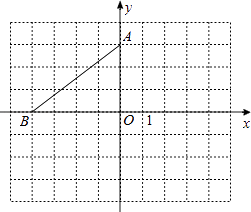
(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.
(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.
【答案】
(1)
解:∵△AOB绕点A逆时针旋转90°后得到△AEF,
∴AO⊥AE,AB⊥AF,BO⊥EF,AO=AE,AB=AF,BO=EF,
∴△AEF在图中表示为:
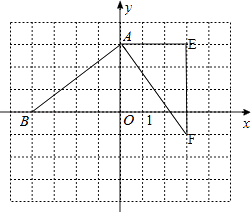
∵AO⊥AE,AO=AE,
∴点E的坐标是(3,3),
∵EF=OB=4,
∴点F的坐标是(3,﹣1)
(2)
解:∵点F落在x轴的上方,
∴EF<AO,
又∵EF=OB,
∴OB<AO,AO=3,
∴OB<3,
∴一个符合条件的点B的坐标是(﹣2,0)
【解析】(1)△AOB绕点A逆时针旋转90°后得到△AEF,所以AO⊥AE,AB⊥AF,BO⊥EF,AO=AE,AB=AF,BO=EF,据此在图中画出△AEF,并写出点E、F的坐标即可.(2)根据点F落在x轴的上方,可得EF<AO;然后根据EF=OB,判断出OB<3,即可求出一个符合条件的点B的坐标是多少.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.