��Ŀ����
����Ŀ���۲�������������
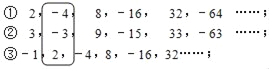
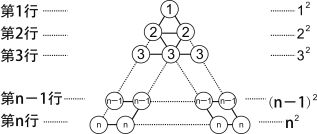
ȡÿһ�еĵ�n���������μ�Ϊx��y��z������ͼ�У���n=2ʱ��x=��4��y=��3��z=2��
��1����n=7ʱ����ֱ��д��x��y��z��ֵ��������������������������С�����IJ
��2����֪nΪż������x��y��z��������������������С�����IJ�Ϊ384����n��ֵ��
��3����m=x+y+z����x��y��z��������������������С�����IJ�Ϊ�� �����ú�m��ʽ�ӱ�ʾ��
���𰸡���1��x=128��y=129��z=��64��������������������С�����IJ�Ϊ193����2��n=8����3����nΪ����ʱ��Ϊm����nΪż��ʱ��Ϊ1��m��
��������
��1��������֪���֣������е������ӵڶ�������ʼ������һ������ǰ��һ�����˩�2�õ��ģ������е��������ж�Ӧ������1�������е���Ϊ�����ж�Ӧ������һ����෴�������˷ֱ����x��y��z��ֵ��������⼴�ɣ�
��2�������жϳ�nΪż��ʱ��z���x��С�������z��x=��![]() x��x=��
x��x=��![]() x������x��y��z��������������������С�����IJ�Ϊ384�г����̣��������n��ֵ��
x������x��y��z��������������������С�����IJ�Ϊ384�г����̣��������n��ֵ��
��3������m=x+y+z���m=��![]() ������2��n+1���ٷ�nΪ������nΪż������������ۼ��ɣ�
������2��n+1���ٷ�nΪ������nΪż������������ۼ��ɣ�
��1���������⣬��x=������2��7=128��y=������2��7+1=129��z=��![]() ��[������2��7]=��64��
��[������2��7]=��64��
��������������������С�����IJ�Ϊ��129������64��=193��
��2����nΪż��ʱ��x��y��0��z��0��
��z=��![]() x��
x��
��z��x=��![]() x��x=��
x��x=��![]() x=384��
x=384��
��x=��256��
�ߩ�����2��8=��256��
��n=8��
��3��m=x+y+z=������2��n+[������2��n+1]+{��![]() ��[������2��n]}
��[������2��n]}
=������2��n������2��n+1+![]() ������2��n
������2��n
=��![]() ������2��n+1��
������2��n+1��
����nΪ����ʱ��y��x��z��
y��z=[������2��n+1]��{��![]() ��[������2��n]}
��[������2��n]}
=������2��n+1��![]() ������2��n
������2��n
=��![]() ������2��n+1
������2��n+1
=m��
����nΪż��ʱ��z��y��x��
z��x={��![]() ��[������2��n]}��[������2��n]
��[������2��n]}��[������2��n]
=![]() ������2��n+����2��n
������2��n+����2��n
=![]() ������2��n
������2��n
=1��m��
�ʴ�Ϊ��nΪ����ʱ��Ϊm����nΪż��ʱ��Ϊ1��m��

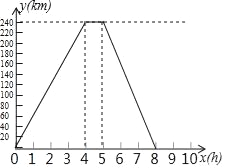
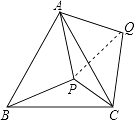
����Ŀ��һ�������A�س�������һ����������Ľֵ���������ÿ����ʻ�����������Ϊ������¼���£�x��5��x��14����λ��m����
��ʻ���� | ��һ�� | �ڶ��� | ������ | ���Ĵ� |
��ʻ��� | x | �� | x��3 | 2��5��x�� |
��ʻ���������������������� | �� �� | �� �� | �� �� | �� �� |
��1���뽫����������
��2��������4����ʻ������������ڵ�λ�ã�
��3���������ʻ����·��Ϊ41m�����һ����ʻ��·��x��ֵ��