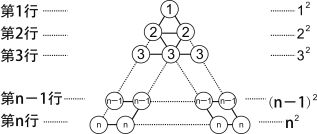
��Ŀ����
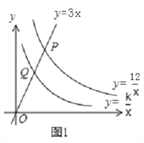
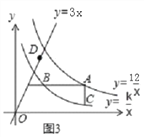
����Ŀ����ͼ1����ֱ֪��y=3x�ֱ���˫����y=![]() ��y=
��y=![]() ��x��0������P��Q���㣬��OP=2OQ��
��x��0������P��Q���㣬��OP=2OQ��
��1����k��ֵ��
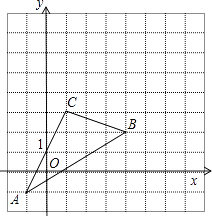
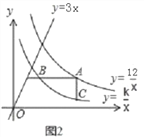
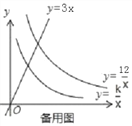
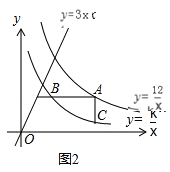
��2����ͼ2������A��˫����y= ![]() �ϵĶ��㣬AB��x�ᣬAC��y�ᣬ�ֱ�˫����y=
�ϵĶ��㣬AB��x�ᣬAC��y�ᣬ�ֱ�˫����y=![]() ��x��0���ڵ�B��C������BC������̽���ڵ�A�˶������У���ABC������Ƿ�仯�������䣬�������ABC����������ı䣬��˵�����ɣ�
��x��0���ڵ�B��C������BC������̽���ڵ�A�˶������У���ABC������Ƿ�仯�������䣬�������ABC����������ı䣬��˵�����ɣ�
��3����ͼ3������D��ֱ��y=3x�ϵ�һ�㣬�����һ��̽���ڵ�A�˶������У��Ե�A��B��C��DΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ������ʱ��A�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��P��2,6�� Q(1,3)��k=3����2���ڵ�A�˶������У���ABC��������䣬ʼ�յ���![]() ��
��
��3������A��B��C��DΪ������ı���Ϊƽ���ı���ʱ����ʱ��A������Ϊ��2![]() ��
��![]() ����2��6����
����2��6����![]() ��6
��6![]() ����
����
����������1���������P�����꣬�ٴ�����OP=2OQ�������������������Σ����Q�����꣬�Ϳ������k��ֵ.
��2�����A�������Ϊ��a,b������b=![]() �������������a�Ĵ���ʽ��ʾ��B����C�����꣬������ʾ���߶�AB��AC�ij����Ϳ������BAC�������һ����ֵ.
�������������a�Ĵ���ʽ��ʾ��B����C�����꣬������ʾ���߶�AB��AC�ij����Ϳ������BAC�������һ����ֵ.
��3���Ե�A��B��C��DΪ������ı���Ϊƽ���ı��οɷֳ����ࣺ��ACΪƽ���ı��ε�һ�ߣ���ACΪƽ���ı��εĶԽ��ߣ�Ȼ������ƽ���ı��ε����ʽ�������a�ķ��̣��������a��ֵ���Ӷ������A������.
��1��P��2,6�� Q(1,3)��k=3.
��2����ͼ2��
��S��ABC=![]() ABAC=
ABAC=![]() ��
��![]() ��
��![]() .
.
���ڵ�A�˶������У���ABC��������䣬ʼ�յ���![]() ��
��
��3����ACΪƽ���ı��ε�һ�ߣ�
��������B�ڵ�Q���ұ�ʱ����ͼ3��
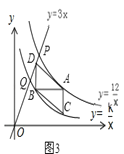
���ı���ACBD��ƽ���ı��Σ���AC��BD��AC=BD����xD=xB=![]() ��
��
��yD=3xD=![]() ����DB=
����DB=![]() .
.
��AC=![]() ����
����![]() =
=![]() ����ã�a=��2
����ã�a=��2![]() ��
��
�����飺a=��2![]() �Ǹ÷��̵Ľ⣮��a��0����a=2
�Ǹ÷��̵Ľ⣮��a��0����a=2![]() ����b=
����b=![]() .
.
���A��������2![]() ��
��![]() ����
����
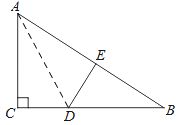
��������B�ڵ�Q������ҵ�C�ڵ�Q���ұ�ʱ����ͼ4��
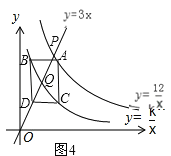
���ı���ACDB��ƽ���ı��Σ���AC��BD��AC=BD��
��xD=xB=![]() ����yD=3xD=
����yD=3xD=![]() ����DB=
����DB=![]() .
.
��AC=![]() ����
����![]() =
=![]() ����ã�a=��2��
����ã�a=��2��
�����飺a=��2�Ǹ÷��̵Ľ⣮
��a��0����a=2����b=![]() =6��
=6��
���A��������2��6����
��ACΪƽ���ı��εĶԽ��ߣ�
��ʱ��B����C���ڵ�Q����ߣ���ͼ5��
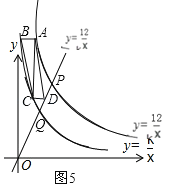
���ı���ABCD��ƽ���ı��Σ�
��AB��CD��AB=CD����yD=yC=![]() ����xD=
����xD=![]() ��
��
��CD=![]() ��a����AB=a��
��a����AB=a��![]() ����
����![]() =
=![]() ��a��
��a��
��ã�a=��![]() ��
��
�����飺a=��![]() �Ǹ÷��̵Ľ⣮
�Ǹ÷��̵Ľ⣮
��a��0����a=![]() ����b=
����b=![]() =6
=6![]() ��
��
���A��������![]() ��6
��6![]() ����
����
��������������A��B��C��DΪ������ı���Ϊƽ���ı���ʱ����ʱ��A������Ϊ��2![]() ��
��![]() ����2��6����
����2��6����![]() ��6
��6![]() ����
����

 �Ͻ�ƽ��У����ϵ�д�
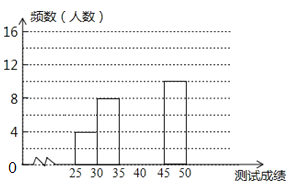
�Ͻ�ƽ��У����ϵ�д�����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�������ٰ�����������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 4 |
��2�� | 30��x��35 | 6 |
��3�� | 35��x��40 | 14 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
����ͼ��������и��⣺
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������40��Ϊ���㣬�β��Ե��������Ƕ��٣�