题目内容
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,超过部分按2.6元/m3计费。设每户家庭用水量为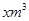 时,应交水费y元。
时,应交水费y元。
(1)分别求出 和
和 时y与x的关系式;
时y与x的关系式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |
y=2.6x-12;小明家这个季度共用水53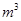
解析试题分析:(1)因为月用水量不超过20m3时,按2元/m3计费,所以当0≤x≤20时,y与x的函数表达式是y=2x;因为月用水量超过20m3时,其中的20m3仍按2元/m3收费,超过部分按2.6元/m3计费,所以当x>20时,y与x的函数表达式是y=2×20+2.6(x-20),即y=2.6x-12;
(2)由题意可得:因为四月份、五月份缴费金额不超过40元,所以用y=2x计算用水量;六月份缴费金额超过40元,所以用y=2.6x-12计算用水量
试题解析:解:(1)当0≤x≤20时,y与x的函数表达式是:y=2x;
当x>20时,y与x的函数表达式是:y=2×20+2.6(x-20)=2.6x-12;
(2)因为小明家四、五月份的水费都不超过40元,故0≤x≤20,此时y=2x,
六月份的水费超过40元,x>20,此时y=2.6x-12,
所以把y=30代入y=2x中得,
2x=30,x=15;
把y=34代入y=2x中得,
2x=34,x=17;
把y=42.6代入y=2.6x-12中得,
2.6x-12=42.6,x=21.
所以,15+17+21=53.
答:小明家这个季度共用水53m3
考点:一次函数的应用

某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
| 原料名称 饮料名称 | 甲 | 乙 |
| A | 20克 | 40克 |
| B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
 和
和 的图像交于点P(-2,-5),则根据图像可得不等式
的图像交于点P(-2,-5),则根据图像可得不等式 的解集是 .
的解集是 .
 与反比例函数
与反比例函数 的图象交点的横坐标为x0.若k<x0<k+1,则整数k的值是 .
的图象交点的横坐标为x0.若k<x0<k+1,则整数k的值是 .


 x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 .
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 . 