��Ŀ����
��һ��ֱ����������A��B��C�����ۿڣ��ס�������ͬʱ�ֱ��A��B�ۿڳ�������ֱ������ʻ��C�ۣ����յ���C�ۣ���ס���������ʻx��h������B�۵ľ���ֱ�Ϊy1��y2��km����y1��y2��x�ĺ�����ϵ��ͼ��
��1����գ�A��C���ۿڼ�ľ���Ϊ km��a= ��
��2����ֱ����y1��y2��x�ĺ�����ϵʽ�����������P�����ꣻ
��3���������ľ��벻����10kmʱ�ܹ����������ס������������ʱ���������10ǧ�ף�
��1��120��4����2��y1= ��y2=15x��0��x��6������P������Ϊ��2��30������3���ס�����������
��y2=15x��0��x��6������P������Ϊ��2��30������3���ס����������� Сʱ��
Сʱ�� Сʱ��
Сʱ�� Сʱ���������10ǧ�ף�
Сʱ���������10ǧ�ף�
���������������1����ͼ�п��Կ���A��B������30km��B��C������90km��A��C���ۿڼ�ľ���Ϊ30+90=120km������·�̡�ʱ��������ٶȣ�30��1=30��km/h�����������a��ֵ��a=120��30=4��
��2�����ô���ϵ�������y1��y2�������ⷽ���飬���������P�����꣮
��3���ȸ���һ�κ�����ͼ������ҵ��ٶȣ��ٸ��ݼ����Ҵ�ǰ���Ҵ����״��Ѿ����˶��Ҵ�������ʻ������������н�ɣ�
�����������1��120��4.
��2����0��x��1ʱ���ɵ㣨0��30������1��0�����y1=��30x+30��
��1��x��4ʱ���ɵ㣨1��0������4��90�����y1=30x��30��
��y1��x�ĺ�����ϵʽΪy1= .
.
�ɵ㣨6��90����ã�y2=15x��0��x��6����
��y2��x�ĺ�����ϵʽΪy2=15x��0��x��6����
��ͼ���֪������P�ĺ�����x��1����ʱy1=y2��
�ⷽ���� ����
���� .
.
���Ե�P������Ϊ��2��30����
��3���ɺ���ͼ���֪���Ҵ����ٶ�Ϊ��90��6=15��km/m����
�ټ����Һ�10km������ʻʱ��Ϊxh����x��2��
���0��x��1����ô����30x+30��+15x=10�����x= ������������ȥ��
������������ȥ��
���1��x��2����ô15x����30x��30��=10�����x= ���������⣻
���������⣻
�ڼ׳����Һ�����ǰ10km������ʻʱ��Ϊxh����x��2��
�����⣬��30x��30��15x=10�����x= ���������⣻
���������⣻
�ۼ״��Ѿ����˶��Ҵ�������ʻ����4��x��6��
�����⣬��90��15x=10�����x= ���������⣻
���������⣻
���ס����������� Сʱ��
Сʱ�� Сʱ��
Сʱ�� Сʱ���������10ǧ�ף�
Сʱ���������10ǧ�ף�
���㣺1.һ�κ�����Ӧ�ã�2.ֱ���ϵ�������뷽�̵Ĺ�ϵ��3.����ϵ������Ӧ�ã�4.����˼���Ӧ��..

 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�ij��Ϊ�˹��������Լ��ˮ�����÷ֶμƷѵķ������¼���ÿ����ͥ��ˮ�ѣ�����ˮ��������20m3ʱ����2Ԫ/m3���㣻����ˮ������20m3ʱ���������ְ�2.6Ԫ/m3�Ʒѡ���ÿ����ͥ��ˮ��Ϊ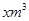 ʱ��Ӧ��ˮ��yԪ��
ʱ��Ӧ��ˮ��yԪ��
��1���ֱ���� ��
�� ʱy��x�Ĺ�ϵʽ��
ʱy��x�Ĺ�ϵʽ��
��2��С���ҵڶ����Ƚ���ˮ�ѵ�������£�
| �·� | ���·� | ���·� | ���·� |
| ���ѽ�� | 30Ԫ | 34Ԫ | 42.6Ԫ |
�±��У�y��x��һ�κ�����
| x |  2 2 | 1 | 2 | | 5 |
| y | 6 |  3 3 | |  12 12 |  15 15 |
��1����ú����ı���ʽ������ȫ����
��2����֪�ú���ͼ����һ��M��1��-3��Ҳ�ڷ���������
 ͼ���ϣ�������������ͼ�����һ����N�����꣮
ͼ���ϣ�������������ͼ�����һ����N�����꣮  ��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�
��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�

 �ڵ�һ�����ڵ�ͼ���ڵ�B��m��n��������OB����S��AOB=6��S��BOC=2��
�ڵ�һ�����ڵ�ͼ���ڵ�B��m��n��������OB����S��AOB=6��S��BOC=2��
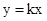 ���ᾭ��һ���̶��ĵ�
���ᾭ��һ���̶��ĵ� �����Ǿͳ�ֱ��
�����Ǿͳ�ֱ�� ȡ�κ�ʵ����������
ȡ�κ�ʵ���������� �������
������� ��ֱ��д������A�����ꣻ
��ֱ��д������A�����ꣻ ���ҡ�B����C�Ľ�ƽ���߷ֱ���y���ֱ��
���ҡ�B����C�Ľ�ƽ���߷ֱ���y���ֱ�� �����BC����ֱ�ߵı���ʽ��
�����BC����ֱ�ߵı���ʽ��
