Question

【题目】抛物线y=ax2+bx﹣4与x轴交于A，B两点，（点B在点A的右侧）且A，B两点的坐标分别为（﹣2，0）、（8，0），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q，交BD于点M．

（1）求抛物线的解析式；
（2）当点P在线段OB上运动时，试探究m为何值时，四边形CQMD是平行四边形？
（3）在（2）的结论下，试问抛物线上是否存在点N（不同于点Q），使三角形BCN的面积等于三角形BCQ的面积？若存在，请求出点N的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：将A（﹣2，0），B（8，0）代入抛物线y=ax2+bx﹣4得：

，

解得： ，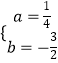

∴抛物线的解析式：y= x2﹣ x﹣4

（2）

解：当x=0时，y=﹣4，

∴C（0，﹣4），

∴OC=4，

∵四边形DECB是菱形，

∴OD=OC=4，

∴D（0，4），

设BD的解析式为：y=kx+b，

把B（8，0）、D（0，4）代入得： ，

解得： ，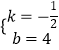

∴BD的解析式为：y=﹣ x+4，

∵l⊥x轴，

∴M（m，﹣ m+4）、Q（m， m2﹣ m﹣4），

如图1，∵MQ∥CD，

∴当MQ=DC时，四边形CQMD是平行四边形，

∴（﹣ m+4）﹣（ m2﹣ m﹣4）=4﹣（﹣4），

化简得：m2﹣4m=0，

解得m1=0（不合题意舍去），m2=4，

∴当m=4时，四边形CQMD是平行四边形

（3）

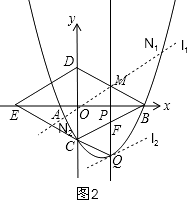
解：如图2，要使三角形BCN的面积等于三角形BCQ的面积，N点到BC的距离与Q到BC的距离相等；

设直线BC的解析式为：y=kx+b，

把B（8，0）、C（0，﹣4）代入得： ，

解得： ，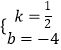

∴直线BC的解析式为：y= x﹣4，

由（2）知：当P（4，0）时，四边形DCQM为平行四边形，

∴BM∥QC，BM=QC，

得△MFB≌△QFC，

分别过M、Q作BC的平行线l1、l2，

所以过M或Q点的斜率为的 直线与抛物线的交点即为所求，

当m=4时，y=﹣ m+4=﹣ ×4+4=2，

∴M（4，2），

当m=4时，y= m2﹣ m﹣4= ×16﹣ ×4﹣4=﹣6，

Q（4，﹣6），

①设直线l1的解析式为：y= x+b，

∵直线l1过Q点时，

∴﹣6= ×4+b，b=﹣8，

∴直线l1的解析式为：y= x﹣8，

则 ，

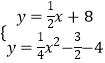= x﹣8，

解得x1=x2=4（与Q重合，舍去），

②∵直线l2过M点，

同理求得直线l2的解析式为：y= x，

则 ，

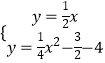= x，

x2﹣x﹣16=0，

解得x1=4+4 ，x2=4﹣4 ，

代入y= x，得 ， ，

则N1（4+4 ，2+2 ），N2（4﹣4 ，2﹣2 ），

故符合条件的N的坐标为N1（4+4 ，2+2 ），N2（4﹣4 ，2﹣2 ）．

【解析】（1）直接将A、B两点的坐标代入抛物线的解析式中，列方程组可求a、b的值，写出解析式即可；（2）先求点C和D的坐标，求直线BD的解析式，根据横坐标m表示出点Q和M的纵坐标，由MQ∥CD，根据一组对边平行且相等的四边形是平行四边形，证明MQ=CD即可，因此列等式：（﹣ m+4）﹣（ m2﹣ m﹣4）=4﹣（﹣4），求m即可；（3）要使三角形BCN的面积等于三角形BCQ的面积，可先判断四边形CQBM是平行四边形，解得M点到BC的距离与Q到BC的距离相等，所以过M或Q点的与直线BC平行的直线与抛物线的交点即为所求，列方程组可得结论．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．