题目内容
【题目】如图所示，在△ABD中，∠A是直角，AB=3，AD=4，BC=12，DC=13，求四边形ABCD的面积.
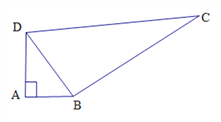
【答案】36
【解析】试题分析：根据勾股定理求得BD=5；由勾股定理的逆定理判定△BCD为直角三角形，则四边形ABCD的面积=△ABD的面积+△BCD的面积．
试题解析：∵在△ABD中，∠A是直角，AB=3，AD=4，
∴由勾股定理得 BD2=AD2+AB2=25．则BD=5，
又∵在△BCD中，BC=12，DC=13，
∴CD2=BD2+BC2=169，
∴△BCD为直角三角形，且∠DBC=90°，
∴S四边形ABCD=S△ABD+S△BCD=
ADAB+
BDBC=
×4×3+
×5×12=36．
即四边形ABCD的面积是36．
考点: 1.勾股定理；2.勾股定理的逆定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：
组号 | 分组 | 频数 |
一 | 6≤m＜7 | 2 |
二 | 7≤m＜8 | 7 |
三 | 8≤m＜9 | a |
四 | 9≤m≤10 | 2 |
（1）求a的值；
（2）若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；
（3）将在第一组内的两名选手记为：A1、A2 ， 在第四组内的两名选手记为：B1、B2 ， 从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．
【题目】下表记录的是流花河今年某一周内的水位变化情况，上周末（星期六）的水位已达到警戒水位
米．（正号表示水位比前一天上升，负号表示水位比前一天下降）
星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
水位变化 |
|
|
|
|
|
|
|
本周哪一天河流的水位最高？哪一天河流的水位最低？它们位于警戒水位之上还是之下？
与上周末相比，本周末河流的水位是上升了还是下降了？
