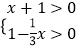题目内容
【题目】如图，一辆汽车从P处出发，先沿北偏东60°的方向行驶到达A处后，接着向正南方向行驶100（ 
+1）千米到达B处．在B处观测到出发时所在的P处在北偏西45°方向上，P，A两处相距多少千米？
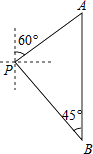
【答案】解：如图作PC⊥AB于C．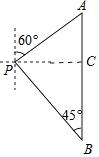
设AC=x千米．
在Rt△PAC中，∵∠A=60°，
∴PC=ACtan60°= 
x，PA= 
=2x，
在Rt△PBC中，∵∠B=45°，
∴BC=PC= x，
∵AC+BC=AB，
∴x+ x=100（ +1），
∴x=100，
∴PA=2x=200，
答：P，A两处相距200千米．
【解析】如图作PC⊥AB于C．设AC=x千米．求出AC、BC，根据AB的长列出方程即可解决问题．
【考点精析】掌握关于方向角问题是解答本题的根本，需要知道指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角．
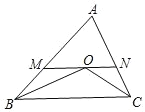
【题目】如图，在△ABC 中，∠ABC、∠ACB 的角平分线交于点 O，MN 过点 O，且MN∥BC，分别交 AB、AC 于点 M、N．若 MN=5cm，CN=2cm，则 BM=________cm．
【题目】“世界那么大，我想去看看”一句话红遍网络，骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场．某车行经营的A型车2016年4月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售价比去年增加400元，若今年4月份与去年4月份卖出的A型车数量相同，则今年4月份A型车销售总额将比去年4月份销售总额增加25%．（A、B两种型号车今年的进货和销售价格如下表所示）
A型车 | B型车 | |
进货价格（元/辆） | 1100 | 1400 |
销售价格（元/辆） | 今年的销售价格 | 2400 |
（1）求今年4月份A型车每辆销售价多少元（用列方程进行解答）；
（2）该车行计划5月份新进一批A型车和B型车共50辆，设购进的A型车为x辆，获得的总利润为y元，请写出y与x之间的函数关系式；
（3）在（2）的条件下，若B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最大？最大利润是多少？
